图

图(graph)是一种非线性数据结构，由顶点(vertex)和边(edge)组成。我们可以将图G抽象地表示为一组顶点V和一组边E的集合。以下示例展示了一个包含5个顶点和7条边的图: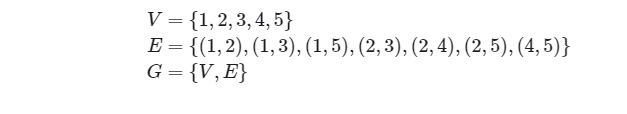
如果将顶点看作节点，将边看作连接各个节点的引用(指针)，我们就可以将图看作一种从链表拓展而来的数据结构。如图所示，相较于线性关系(链表)和分治关系(树)，网络关系(图)的自由度更高，因而更为复杂。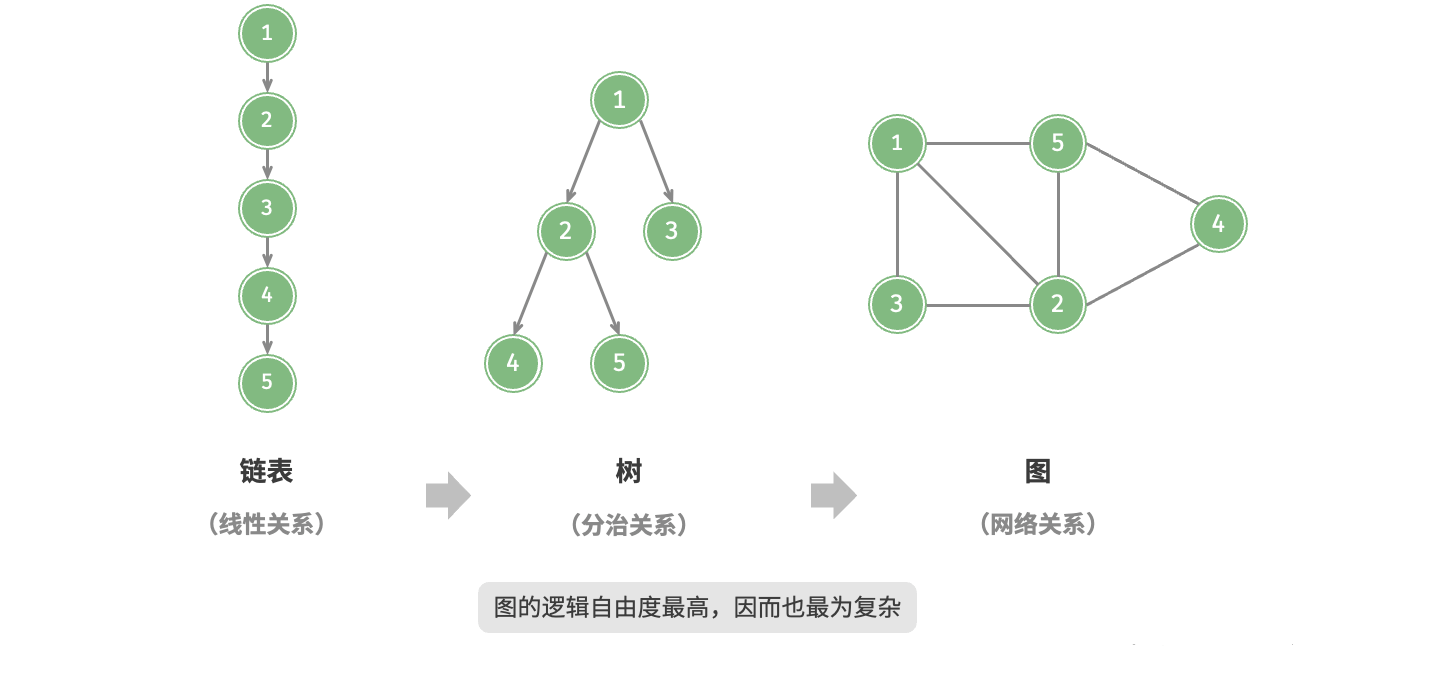

1. 图的常见类型与术语

根据边是否具有方向，可分为无向图(undirected graph)和有向图(directed graph)，如图所示:

1. 在无向图中，边表示两顶点之间的"双向"连接关系，例如微信或QQ中的"好友关系"。
2. 在有向图中，边具有方向性，即A➔B和A🡸B两个方向的边是相互独立的，例如微博或抖音上的"关注"与"被关注"关系。
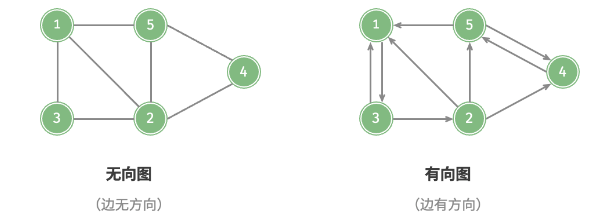   根据所有顶点是否连通，可分为连通图(connected graph)和非连通图(disconnected graph)，如图所示:
   对于连通图，从某个顶点出发，可以到达其余任意顶点。对于非连通图，从某个顶点出发，至少有一个顶点无法到达。
   我们还可以为边添加"权重"变量，从而得到如图所示的有权图(weighted graph)。例如在《王者荣耀》等手游中，系统会根据共同游戏时间来计算玩家之间的"亲密度"，这种亲密度网络就可以用有权图来表示。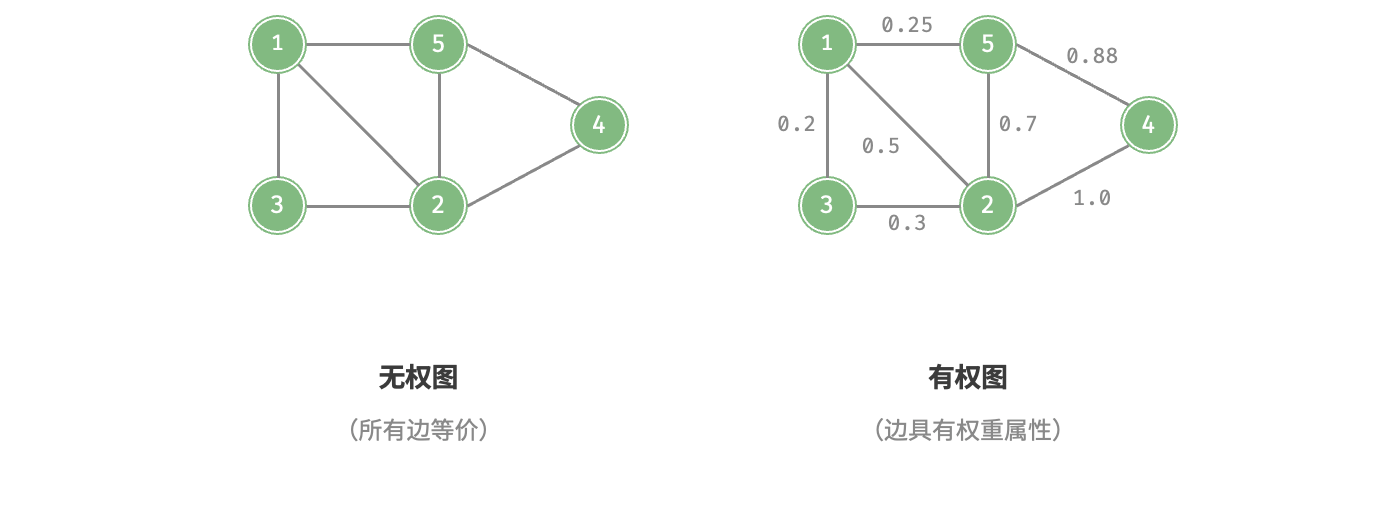
   图数据结构包含以下常用术语:

• 邻接(adjacency)：当两顶点之间存在边相连时，称这两顶点"邻接"。在上图中，顶点1的邻接顶点为顶点2、3、5。
• 路径(path)：从顶点A到顶点B经过的边构成的序列被称为从A到B的"路径"。在上图中，边序列1-5-2-4是顶点1到顶点4的一条路径。
• 度(degree)：一个顶点拥有的边数。对于有向图，入度(in-degree)表示有多少条边指向该顶点，出度(out-degree)表示有多少条边从该顶点指出。

2. 图的表示

图的常用表示方式包括"邻接矩阵"和"邻接表"。以下使用无向图进行举例。

2.1 邻接矩阵

设图的顶点数量为n，邻接矩阵(adjacency matrix)使用一个nxn大小的矩阵来表示图，每一行(列)代表一个顶点，矩阵元素代表边，用1或0表示两个顶点之间是否存在边。如图所示，设邻接矩阵为M、顶点列表为V，那么矩阵元素M[i,j]=1表示顶点V[i]到顶点V[j]之间存在边，反之M[i,j]=0表示两顶点之间无边。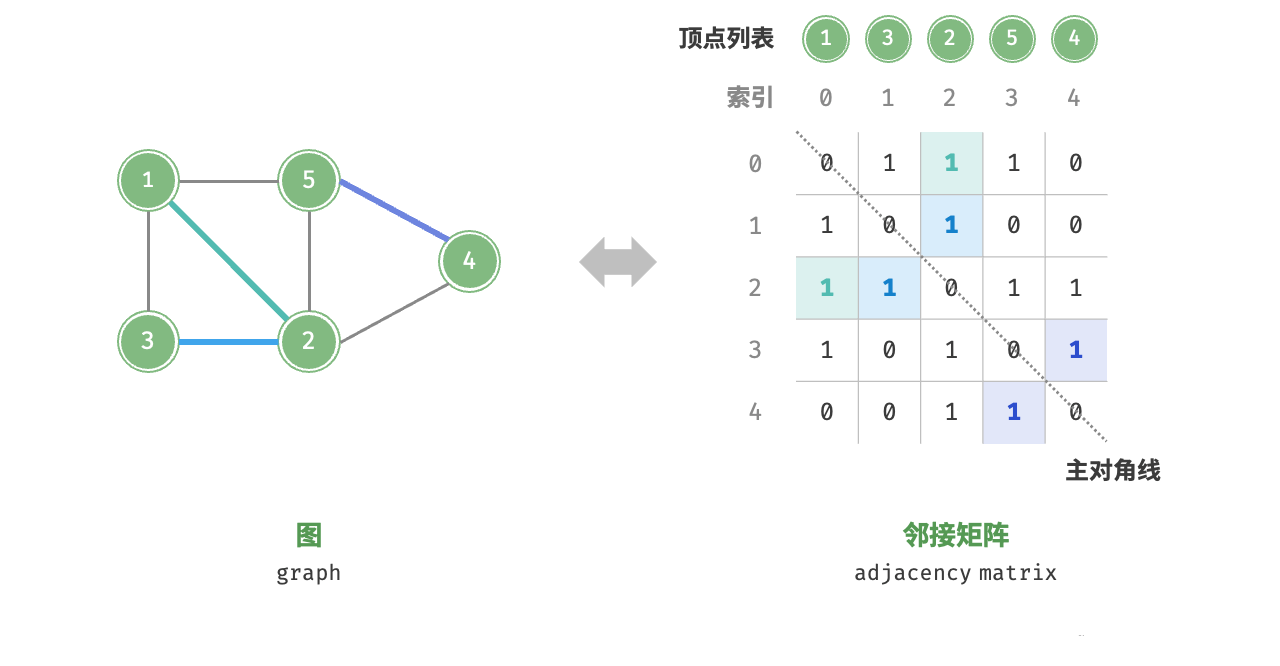
邻接矩阵具有以下特性:
在简单图中，顶点不能与自身相连，此时邻接矩阵主对角线元素没有意义。
对于无向图，两个方向的边等价，此时邻接矩阵关于主对角线对称。
将邻接矩阵的元素从1和0替换为权重，则可表示有权图。
使用邻接矩阵表示图时，我们可以直接访问矩阵元素以获取边，因此增删查改操作的效率很高，时间复杂度均为O(1)。然而，矩阵的空间复杂度为O(n²)，内存占用较多。

2.2 邻接表

邻接表(adjacency list)使用n个链表来表示图，链表节点表示顶点。第i个链表对应顶点i，其中存储了该顶点的所有邻接顶点(与该顶点相连的顶点)。下图展示了一个使用邻接表存储的图的示例。 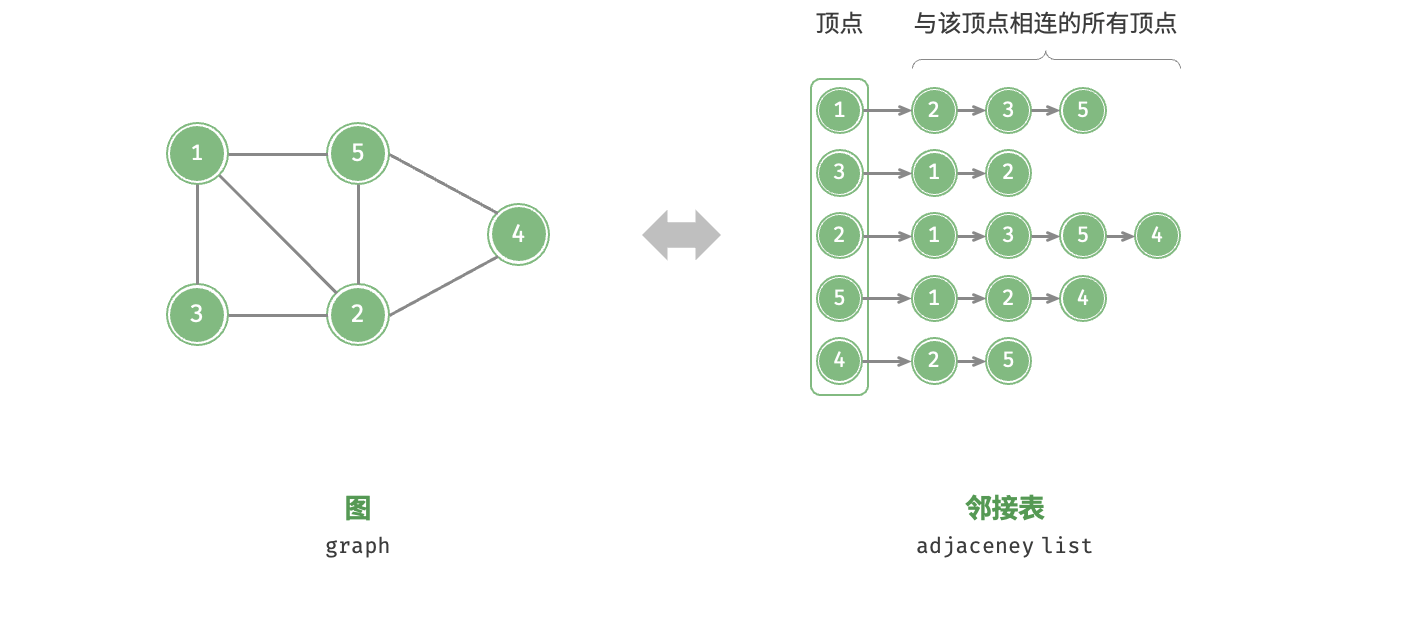邻接表仅存储实际存在的边，而边的总数通常远小于n²，因此它更加节省空间。然而，在邻接表中需要通过遍历链表来查找边，因此其时间效率不如邻接矩阵。邻接表结构与哈希表中的"链式地址"非常相似，因此我们也可以采用类似的方法来优化效率。比如当链表较长时，可以将链表转化为 AVL 树或红黑树，从而将时间效率从O(n)优化至O(logn)；还可以把链表转换为哈希表，从而将时间复杂度降至O(1)。

3. 图的常见应用

	顶点	边	图计算问题
社交网络	用户	好友关系	潜在好友推荐
地铁线路	站点	站点间的连通性	最短路线推荐
太阳系	星体	星体间的万有引力作用	行星轨道计算

4. 图的基础操作

图的基础操作可分为对"边"的操作和对"顶点"的操作。在"邻接矩阵"和"邻接表"两种表示方法下，实现方式有所不同。

4.1 基于邻接矩阵的实现

给定一个顶点数量为n的无向图，则各种操作的实现方式如图所示:

• 添加或删除边：直接在邻接矩阵中修改指定的边即可，使用O(1)时间。而由于是无向图，因此需要同时更新两个方向的边。
• 添加顶点：在邻接矩阵的尾部添加一行一列，并全部填0即可，使用O(n)时间。
• 删除顶点：在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况，需要将(n-1)²个元素"向左上移动"，从而使用O(n²)时间。
• 初始化：传入n个顶点，初始化长度为n的顶点列表vertices，使用O(n)时间；初始化n x n大小的邻接矩阵adjMat ，使用O(n²)时间。
  以下是基于邻接矩阵表示图的实现代码：

/* 基于邻接矩阵实现的无向图类 */
class GraphAdjMat {
    List<Integer> vertices; // 顶点列表，元素代表"顶点值"，索引代表"顶点索引"
    List<List<Integer>> adjMat; // 邻接矩阵，行列索引对应"顶点索引"

    /* 构造方法 */
    public GraphAdjMat(int[] vertices, int[][] edges) {
        this.vertices = new ArrayList<>();
        this.adjMat = new ArrayList<>();
        // 添加顶点
        for (int val : vertices) {
            addVertex(val);
        }
        // 添加边
        // 请注意，edges 元素代表顶点索引，即对应 vertices 元素索引
        for (int[] e : edges) {
            addEdge(e[0], e[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return vertices.size();
    }

    /* 添加顶点 */
    public void addVertex(int val) {
        int n = size();
        // 向顶点列表中添加新顶点的值
        vertices.add(val);
        // 在邻接矩阵中添加一行
        List<Integer> newRow = new ArrayList<>(n);
        for (int j = 0; j < n; j++) {
            newRow.add(0);
        }
        adjMat.add(newRow);
        // 在邻接矩阵中添加一列
        for (List<Integer> row : adjMat) {
            row.add(0);
        }
    }

    /* 删除顶点 */
    public void removeVertex(int index) {
        if (index >= size())
            throw new IndexOutOfBoundsException();
        // 在顶点列表中移除索引 index 的顶点
        vertices.remove(index);
        // 在邻接矩阵中删除索引 index 的行
        adjMat.remove(index);
        // 在邻接矩阵中删除索引 index 的列
        for (List<Integer> row : adjMat) {
            row.remove(index);
        }
    }

    /* 添加边 */
    // 参数 i, j 对应 vertices 元素索引
    public void addEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        // 在无向图中，邻接矩阵关于主对角线对称，即满足 (i, j) == (j, i)
        adjMat.get(i).set(j, 1);
        adjMat.get(j).set(i, 1);
    }

    /* 删除边 */
    // 参数 i, j 对应 vertices 元素索引
    public void removeEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        adjMat.get(i).set(j, 0);
        adjMat.get(j).set(i, 0);
    }

    /* 打印邻接矩阵 */
    public void print() {
        System.out.print("顶点列表 = ");
        System.out.println(vertices);
        System.out.println("邻接矩阵 =");
        PrintUtil.printMatrix(adjMat);
    }
}

4.2 基于邻接表的实现

设无向图的顶点总数为n、边总数为m，则可根据图所示的方法实现各种操作:

• 初始化：在邻接表中创建n个顶点和2m条边，使用O(m+n)时间。
• 添加边：在顶点对应链表的末尾添加边即可，使用O(1)时间。因为是无向图，所以需要同时添加两个方向的边。
• 删除边：在顶点对应链表中查找并删除指定边，使用O(m)时间。在无向图中，需要同时删除两个方向的边。
• 添加顶点：在邻接表中添加一个链表，并将新增顶点作为链表头节点，使用O(1)时间。
• 删除顶点：需遍历整个邻接表，删除包含指定顶点的所有边，使用O(m+n)时间。
  以下是邻接表的代码实现。对比图，实际代码有以下不同:
  为了方便添加与删除顶点，以及简化代码，我们使用列表(动态数组)来代替链表。
  使用哈希表来存储邻接表，key为顶点实例，value为该顶点的邻接顶点列表(链表)。
  另外，我们在邻接表中使用Vertex类来表示顶点，这样做的原因是：如果与邻接矩阵一样，用列表索引来区分不同顶点，那么假设要删除索引为i的顶点，则需遍历整个邻接表，将所有大于i的索引全部减1，效率很低。而如果每个顶点都是唯一的Vertex实例，删除某一顶点之后就无须改动其他顶点了。

/* 基于邻接表实现的无向图类 */
class GraphAdjList {
    // 邻接表，key：顶点，value：该顶点的所有邻接顶点
    Map<Vertex, List<Vertex>> adjList;

    /* 构造方法 */
    public GraphAdjList(Vertex[][] edges) {
        this.adjList = new HashMap<>();
        // 添加所有顶点和边
        for (Vertex[] edge : edges) {
            addVertex(edge[0]);
            addVertex(edge[1]);
            addEdge(edge[0], edge[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return adjList.size();
    }

    /* 添加边 */
    public void addEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 添加边 vet1 - vet2
        adjList.get(vet1).add(vet2);
        adjList.get(vet2).add(vet1);
    }

    /* 删除边 */
    public void removeEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 删除边 vet1 - vet2
        adjList.get(vet1).remove(vet2);
        adjList.get(vet2).remove(vet1);
    }

    /* 添加顶点 */
    public void addVertex(Vertex vet) {
        if (adjList.containsKey(vet))
            return;
        // 在邻接表中添加一个新链表
        adjList.put(vet, new ArrayList<>());
    }

    /* 删除顶点 */
    public void removeVertex(Vertex vet) {
        if (!adjList.containsKey(vet))
            throw new IllegalArgumentException();
        // 在邻接表中删除顶点 vet 对应的链表
        adjList.remove(vet);
        // 遍历其他顶点的链表，删除所有包含 vet 的边
        for (List<Vertex> list : adjList.values()) {
            list.remove(vet);
        }
    }

    /* 打印邻接表 */
    public void print() {
        System.out.println("邻接表 =");
        for (Map.Entry<Vertex, List<Vertex>> pair : adjList.entrySet()) {
            List<Integer> tmp = new ArrayList<>();
            for (Vertex vertex : pair.getValue())
                tmp.add(vertex.val);
            System.out.println(pair.getKey().val + ": " + tmp + ",");
        }
    }
}

4.3 效率对比

设图中共有n个顶点和m条边，下表对比了邻接矩阵和邻接表的时间效率和空间效率：

	邻接矩阵	邻接表(链表)	邻接表(哈希表)
判断是否邻接	O(1)	O(m)	O(1)
添加边	O(1)	O(1)	O(1)
删除边	O(1)	O(m)	O(1)
添加顶点	O(n)	O(1)	O(1)
删除顶点	O(n²)	O(n+m)	O(n)
内存空间占用	O(n²)	O(n+m)	O(n+m)

5. 图的遍历

树代表的是"一对多"的关系，而图则具有更高的自由度，可以表示任意的"多对多"关系。因此，我们可以把树看作图的一种特例。显然，树的遍历操作也是图的遍历操作的一种特例。图和树都需要应用搜索算法来实现遍历操作。图的遍历方式也可分为两种：广度优先遍历和深度优先遍历。

5.1 广度优先遍历

广度优先遍历是一种由近及远的遍历方式，从某个节点出发，始终优先访问距离最近的顶点，并一层层向外扩张。如图所示，从左上角顶点出发，首先遍历该顶点的所有邻接顶点，然后遍历下一个顶点的所有邻接顶点，以此类推，直至所有顶点访问完毕。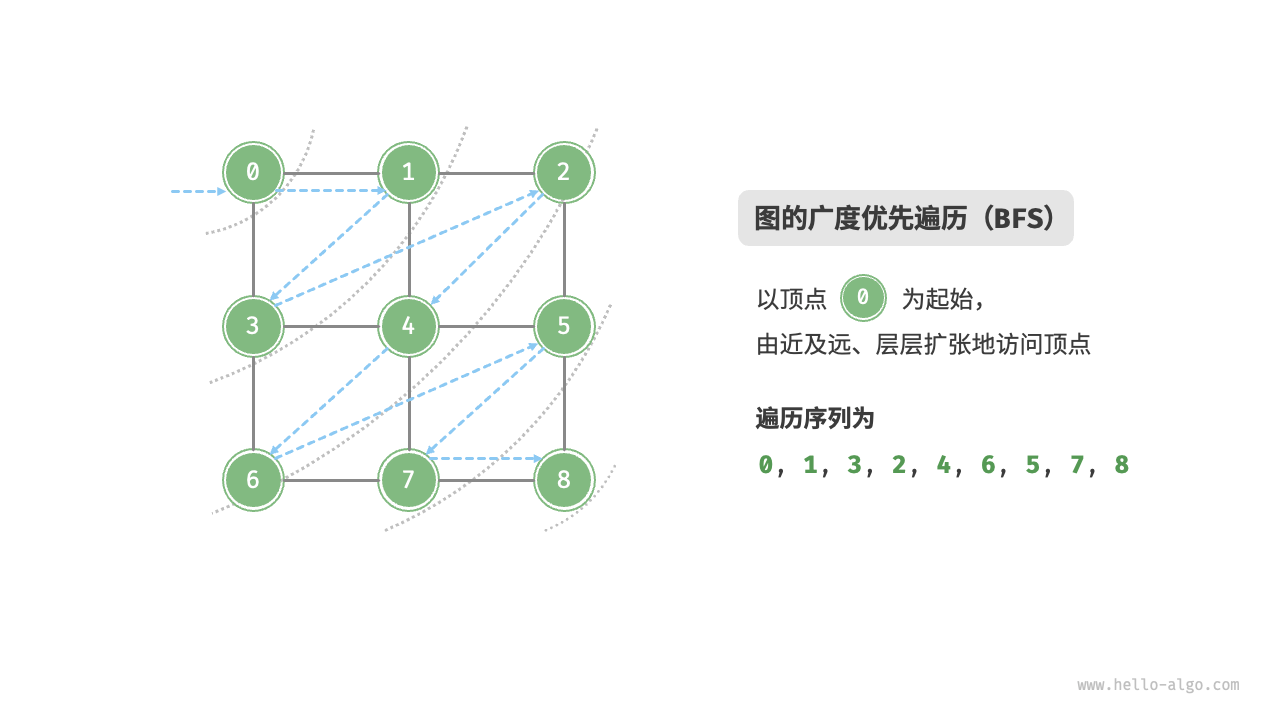

1. 算法实现
   BFS(Breadth-First Search，广度优先搜索)通常借助队列来实现，代码如下所示。队列具有"先入先出"的性质，这与BFS的"由近及远"的思想异曲同工。

• 将遍历起始顶点startVet加入队列，并开启循环。
• 在循环的每轮迭代中，弹出队首顶点并记录访问，然后将该顶点的所有邻接顶点加入到队列尾部。
• 循环步骤2. 直到所有顶点被访问完毕后结束。

为了防止重复遍历顶点，我们需要借助一个哈希集合visited来记录哪些节点已被访问。

提示

哈希集合可以看作一个只存储key而不存储value的哈希表，它可以在O(1)时间复杂度下进行key的增删查改操作。根据key的唯一性，哈希集合通常用于数据去重等场景。

/* 广度优先遍历 */
// 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
List<Vertex> graphBFS(GraphAdjList graph, Vertex startVet) {
    // 顶点遍历序列
    List<Vertex> res = new ArrayList<>();
    // 哈希集合，用于记录已被访问过的顶点
    Set<Vertex> visited = new HashSet<>();
    visited.add(startVet);
    // 队列用于实现 BFS
    Queue<Vertex> que = new LinkedList<>();
    que.offer(startVet);
    // 以顶点 vet 为起点，循环直至访问完所有顶点
    while (!que.isEmpty()) {
        Vertex vet = que.poll(); // 队首顶点出队
        res.add(vet);            // 记录访问顶点
        // 遍历该顶点的所有邻接顶点
        for (Vertex adjVet : graph.adjList.get(vet)) {
            if (visited.contains(adjVet))
                continue;        // 跳过已被访问的顶点
            que.offer(adjVet);   // 只入队未访问的顶点
            visited.add(adjVet); // 标记该顶点已被访问
        }
    }
    // 返回顶点遍历序列
    return res;
}

代码相对抽象，建议对照下图来加深理解: 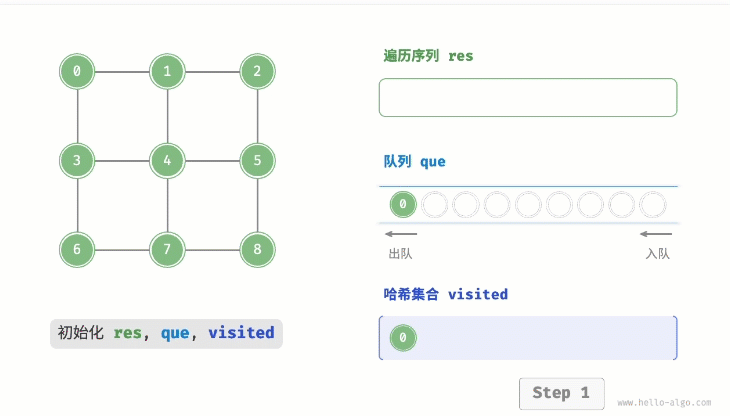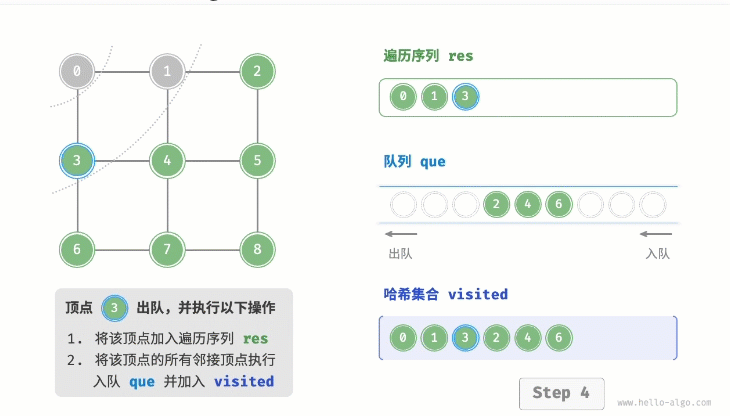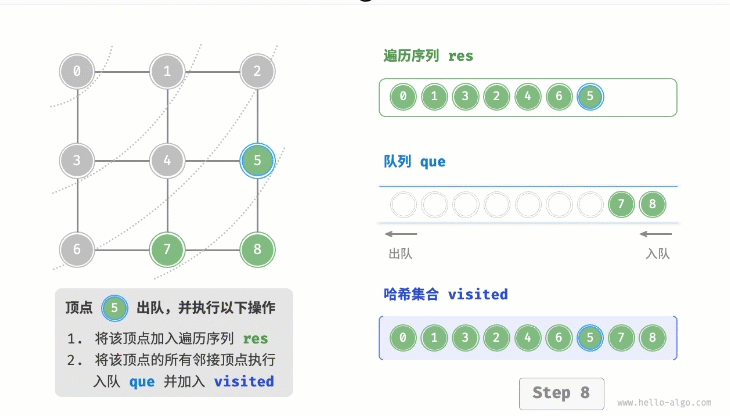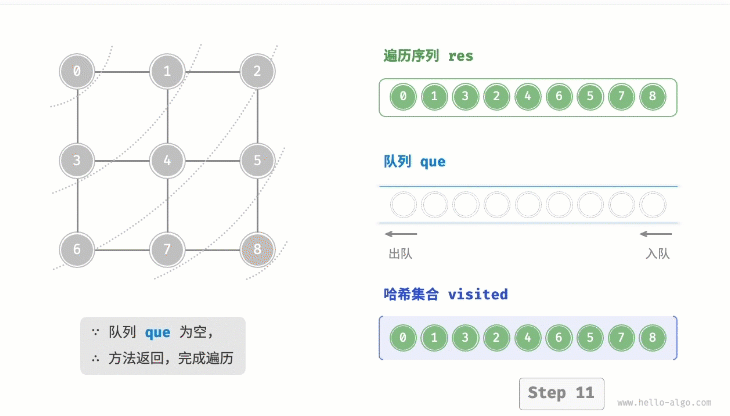2. 复杂度分析
时间复杂度：所有顶点都会入队并出队一次，使用O(|V|)时间；在遍历邻接顶点的过程中，由于是无向图，因此所有边都会被访问2次，使用O(2|E|)时间；总体使用O(|V|+|E|)时间。
空间复杂度：列表res，哈希集合visited，队列que中的顶点数量最多为|V|，使用O(|V|)空间。

5.2 深度优先遍历

深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。如图所示，从左上角顶点出发，访问当前顶点的某个邻接顶点，直到走到尽头时返回，再继续走到尽头并返回，以此类推，直至所有顶点遍历完成。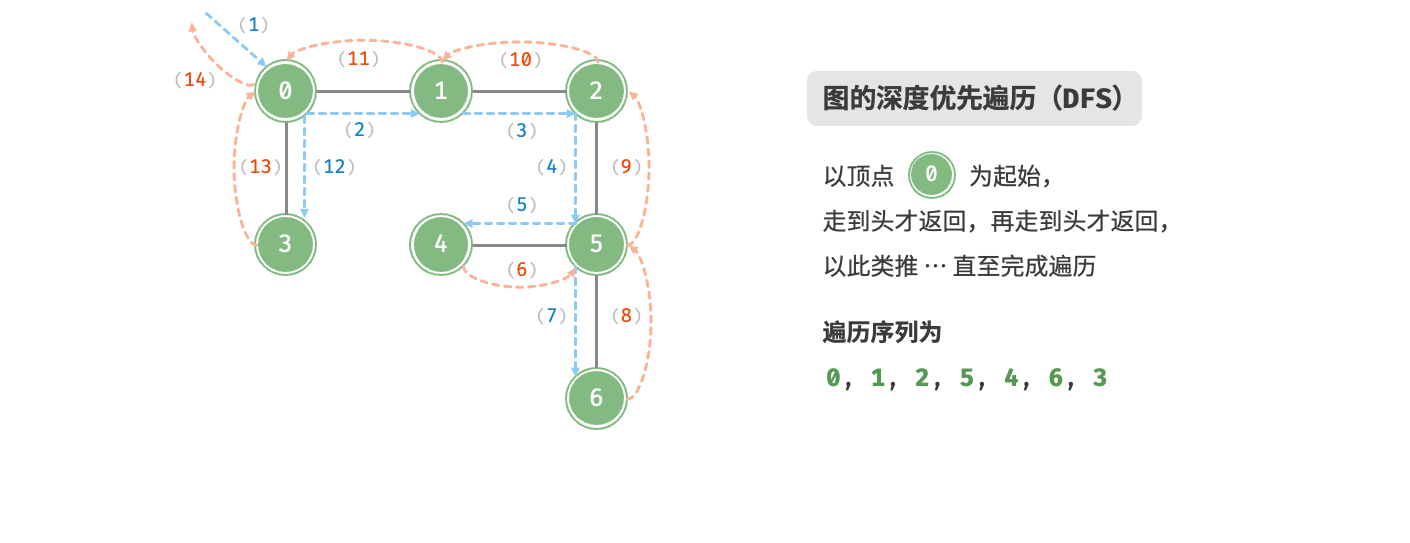

1. 算法实现 这种"走到尽头再返回"的算法范式通常基于递归来实现。与广度优先遍历类似，在深度优先遍历中，我们也需要借助一个哈希集合visited来记录已被访问的顶点，以避免重复访问顶点。

/* 深度优先遍历辅助函数 */
void dfs(GraphAdjList graph, Set<Vertex> visited, List<Vertex> res, Vertex vet) {
    res.add(vet);     // 记录访问顶点
    visited.add(vet); // 标记该顶点已被访问
    // 遍历该顶点的所有邻接顶点
    for (Vertex adjVet : graph.adjList.get(vet)) {
        if (visited.contains(adjVet))
            continue; // 跳过已被访问的顶点
        // 递归访问邻接顶点
        dfs(graph, visited, res, adjVet);
    }
}

/* 深度优先遍历 */
// 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
List<Vertex> graphDFS(GraphAdjList graph, Vertex startVet) {
    // 顶点遍历序列
    List<Vertex> res = new ArrayList<>();
    // 哈希集合，用于记录已被访问过的顶点
    Set<Vertex> visited = new HashSet<>();
    dfs(graph, visited, res, startVet);
    return res;
}

深度优先遍历的算法流程如图所示。

• 直虚线代表向下递推，表示开启了一个新的递归方法来访问新顶点。
• 曲虚线代表向上回溯，表示此递归方法已经返回，回溯到了开启此方法的位置。

为了加深理解，建议将图与代码结合起来，在脑中模拟(或者用笔画下来)整个DFS过程，包括每个递归方法何时开启、何时返回。
2. 复杂度分析
时间复杂度：所有顶点都会被访问1次，使用O(|V|)时间；所有边都会被访问2次，使用O(2|E|)时间；总体使用O(|V|+|E|)时间。
空间复杂度：列表res ，哈希集合visited顶点数量最多为|V|，递归深度最大为|V|，因此使用O(|V|)空间。