分治算法
分治(divide and conquer),全称分而治之,是一种非常重要且常见的算法策略。分治通常基于递归实现,包括"分"和"治"两个步骤:
- 分(划分阶段):递归地将原问题分解为两个或多个子问题,直至到达最小子问题时终止。
- 治(合并阶段):从已知解的最小子问题开始,从底至顶地将子问题的解进行合并,从而构建出原问题的解。
如图所示,"归并排序"是分治策略的典型应用之一。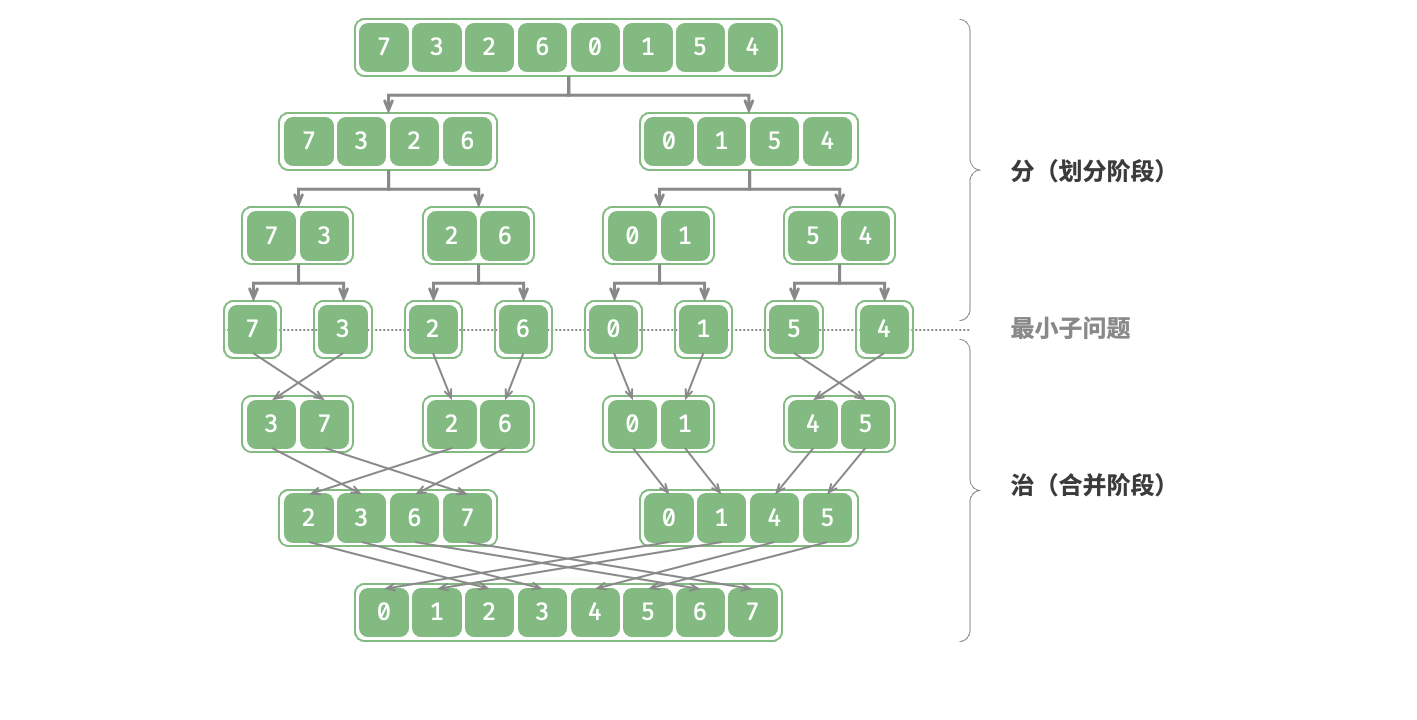
1. 如何判断分治问题
一个问题是否适合使用分治解决,通常可以参考以下几个判断依据:
- 问题可以分解:原问题可以分解成规模更小、类似的子问题,以及能够以相同方式递归地进行划分。
- 子问题是独立的:子问题之间没有重叠,互不依赖,可以独立解决。
- 子问题的解可以合并:原问题的解通过合并子问题的解得来。
2. 通过分治提升效率
分治不仅可以有效地解决算法问题,往往还可以提升算法效率。在排序算法中,快速排序、归并排序、堆排序相较于选择、冒泡、插入排序更快,就是因为它们应用了分治策略。那么,我们不禁发问:为什么分治可以提升算法效率,其底层逻辑是什么?换句话说,将大问题分解为多个子问题、解决子问题、将子问题的解合并为原问题的解,这几步的效率为什么比直接解决原问题的效率更高?这个问题可以从操作数量和并行计算两方面来讨论。
2.1 操作数量优化
以"冒泡排序"为例,其处理一个长度为n的数组需要O(n²)时间。假设我们按照图所示的方式,将数组从中点处分为两个子数组,则划分需要O(n)时间,排序每个子数组需要O((n/2)²)时间,合并两个子数组需要O(n)时间,总体时间复杂度为: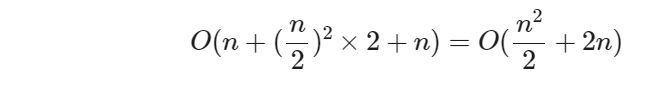
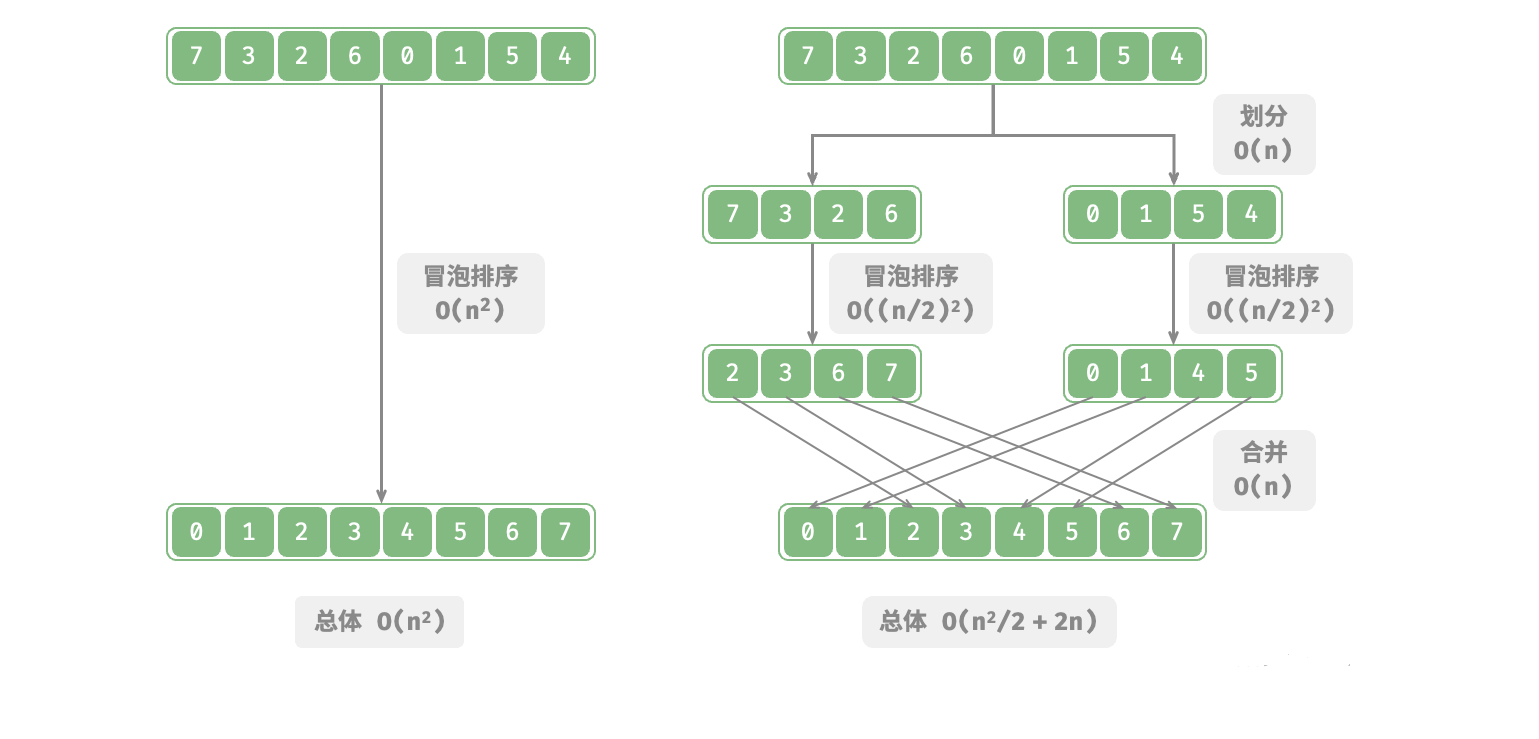 接下来,我们计算以下不等式,其左边和右边分别为划分前和划分后的操作总数:
接下来,我们计算以下不等式,其左边和右边分别为划分前和划分后的操作总数: 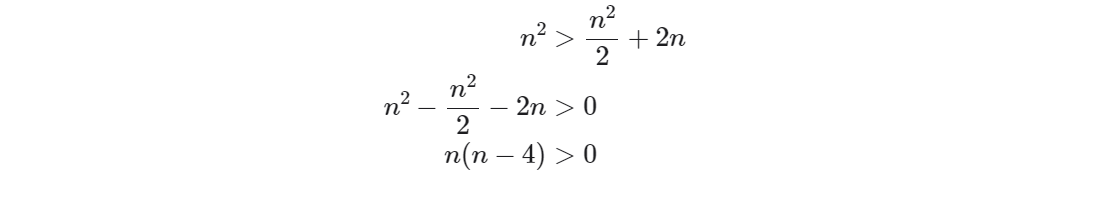 这意味着当n>4时,划分后的操作数量更少,排序效率应该更高。请注意,划分后的时间复杂度仍然是平方阶O(n²),只是复杂度中的常数项变小了。
这意味着当n>4时,划分后的操作数量更少,排序效率应该更高。请注意,划分后的时间复杂度仍然是平方阶O(n²),只是复杂度中的常数项变小了。
进一步想,如果我们把子数组不断地再从中点处划分为两个子数组,直至子数组只剩一个元素时停止划分呢?这种思路实际上就是"归并排序",时间复杂度为O(nlogn)。
再思考,如果我们多设置几个划分点,将原数组平均划分为k个子数组呢?这种情况与"桶排序"非常类似,它非常适合排序海量数据,理论上时间复杂度可以达到O(n+k)。
2.2 并行计算优化
我们知道,分治生成的子问题是相互独立的,因此通常可以并行解决。也就是说,分治不仅可以降低算法的时间复杂度,还有利于操作系统的并行优化。并行优化在多核或多处理器的环境中尤其有效,因为系统可以同时处理多个子问题,更加充分地利用计算资源,从而显著减少总体的运行时间。
比如在图所示的"桶排序"中,我们将海量的数据平均分配到各个桶中,则可将所有桶的排序任务分散到各个计算单元,完成后再合并结果。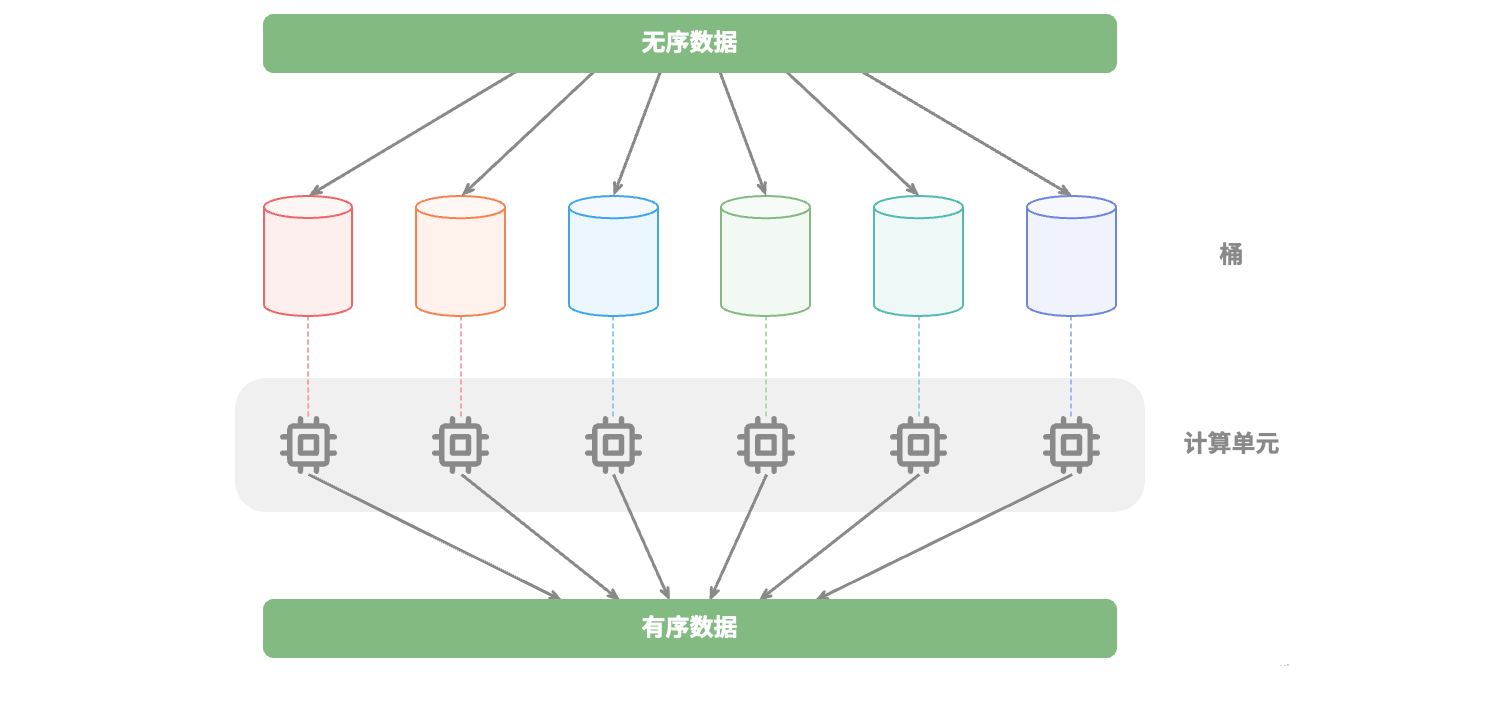
3. 分治常见应用
一方面,分治可以用来解决许多经典算法问题。
- 寻找最近点对:该算法首先将点集分成两部分,然后分别找出两部分中的最近点对,最后找出跨越两部分的最近点对。
- 大整数乘法:例如 Karatsuba 算法,它将大整数乘法分解为几个较小的整数的乘法和加法。
- 矩阵乘法:例如 Strassen 算法,它将大矩阵乘法分解为多个小矩阵的乘法和加法。
- 汉诺塔问题:汉诺塔问题可以通过递归解决,这是典型的分治策略应用。
- 求解逆序对:在一个序列中,如果前面的数字大于后面的数字,那么这两个数字构成一个逆序对。求解逆序对问题可以利用分治的思想,借助归并排序进行求解。
另一方面,分治在算法和数据结构的设计中应用得非常广泛。
- 二分查找:二分查找是将有序数组从中点索引处分为两部分,然后根据目标值与中间元素值比较结果,决定排除哪一半区间,并在剩余区间执行相同的二分操作。
- 归并排序:本节开头已介绍,不再赘述。
- 快速排序:快速排序是选取一个基准值,然后把数组分为两个子数组,一个子数组的元素比基准值小,另一子数组的元素比基准值大,再对这两部分进行相同的划分操作,直至子数组只剩下一个元素。
- 桶排序:桶排序的基本思想是将数据分散到多个桶,然后对每个桶内的元素进行排序,最后将各个桶的元素依次取出,从而得到一个有序数组。
- 树:例如二叉搜索树、AVL 树、红黑树、B 树、B+ 树等,它们的查找、插入和删除等操作都可以视为分治策略的应用。
- 堆:堆是一种特殊的完全二叉树,其各种操作,如插入、删除和堆化,实际上都隐含了分治的思想。
- 哈希表:虽然哈希表并不直接应用分治,但某些哈希冲突解决方案间接应用了分治策略,例如,链式地址中的长链表会被转化为红黑树,以提升查询效率。
可以看出,分治是一种"润物细无声"的算法思想,隐含在各种算法与数据结构之中。
4. 分治搜索策略
我们已经学过,搜索算法分为两大类:
- 暴力搜索:它通过遍历数据结构实现,时间复杂度为O(n)。
- 自适应搜索:它利用特有的数据组织形式或先验信息,时间复杂度可达到O(logn)甚至O(1)。
实际上,时间复杂度为O(logn)的搜索算法通常是基于分治策略实现的,例如二分查找和树。
- 二分查找的每一步都将问题(在数组中搜索目标元素)分解为一个小问题(在数组的一半中搜索目标元素),这个过程一直持续到数组为空或找到目标元素为止。
- 树是分治思想的代表,在二叉搜索树、AVL 树、堆等数据结构中,各种操作的时间复杂度皆为O(logn)。
分治能够提升搜索效率,本质上是因为暴力搜索每轮只能排除一个选项,而分治搜索每轮可以排除一半选项。
4.1 基于分治实现二分查找
- 查找需求
给定一个长度为n的有序数组nums ,其中所有元素都是唯一的,请查找元素target。
从分治角度,我们将搜索区间[i, j]对应的子问题记为f(i,j)。以原问题f(0, n-1)为起始点,通过以下步骤进行二分查找:
- 计算搜索区间[i, j]的中点m, 根据它排除一半搜索区间。
- 递归求解规模减小一半的子问题,可能为f(i, m-1)或f(m+1, j)。
- 循环第1步和第2步,直至找到target或区间为空时返回。
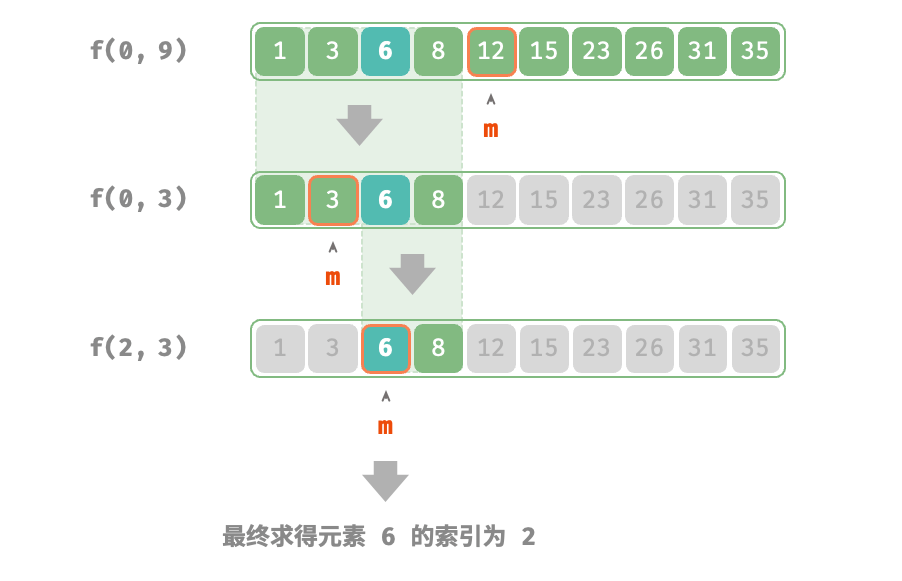
在实现代码中,我们声明一个递归函数dfs()来求解问题f(i,j):
/* 二分查找:问题 f(i, j) */
int dfs(int[] nums, int target, int i, int j) {
// 若区间为空,代表无目标元素,则返回 -1
if (i > j) {
return -1;
}
// 计算中点索引 m
int m = (i + j) / 2;
if (nums[m] < target) {
// 递归子问题 f(m+1, j)
return dfs(nums, target, m + 1, j);
} else if (nums[m] > target) {
// 递归子问题 f(i, m-1)
return dfs(nums, target, i, m - 1);
} else {
// 找到目标元素,返回其索引
return m;
}
}
/* 二分查找 */
int binarySearch(int[] nums, int target) {
int n = nums.length;
// 求解问题 f(0, n-1)
return dfs(nums, target, 0, n - 1);
}5. 构建二叉树问题
5.1 需求
给定一棵二叉树的前序遍历preorder和中序遍历inorder,请从中构建二叉树,返回二叉树的根节点。假设二叉树中没有值重复的节点(如图所示)。 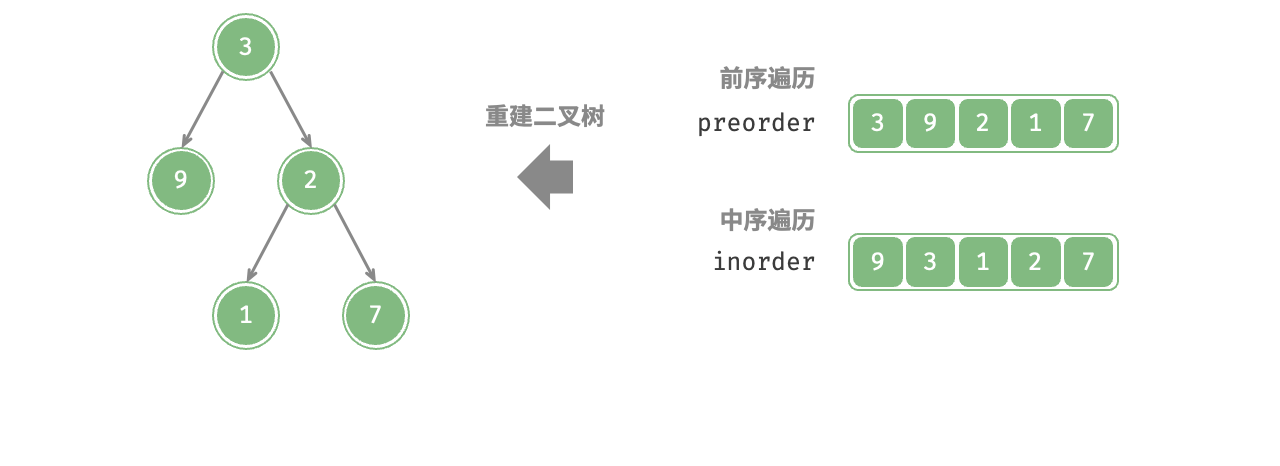
5.2 判断是否为分治问题
原问题定义为从preorder和inorder构建二叉树,是一个典型的分治问题:
- 问题可以分解:从分治的角度切入,我们可以将原问题划分为两个子问题:构建左子树、构建右子树,加上一步操作:初始化根节点。而对于每棵子树(子问题),我们仍然可以复用以上划分方法,将其划分为更小的子树(子问题),直至达到最小子问题(空子树)时终止。
- 子问题是独立的:左子树和右子树是相互独立的,它们之间没有交集。在构建左子树时,我们只需关注中序遍历和前序遍历中与左子树对应的部分。右子树同理。
- 子问题的解可以合并:一旦得到了左子树和右子树(子问题的解),我们就可以将它们链接到根节点上,得到原问题的解。
5.3 如何划分子树
根据以上分析,这道题可以使用分治来求解,但如何通过前序遍历preorder和中序遍历inorder来划分左子树和右子树呢?
根据定义,preorder和inorder都可以划分为三个部分。
前序遍历:[ 根节点 | 左子树 | 右子树 ] ,例如上图中的树对应[ 3 | 9 | 2 1 7 ]。
中序遍历:[ 左子树 | 根节点 | 右子树 ] ,例如上图中的树对应[ 9 | 3 | 1 2 7 ]。
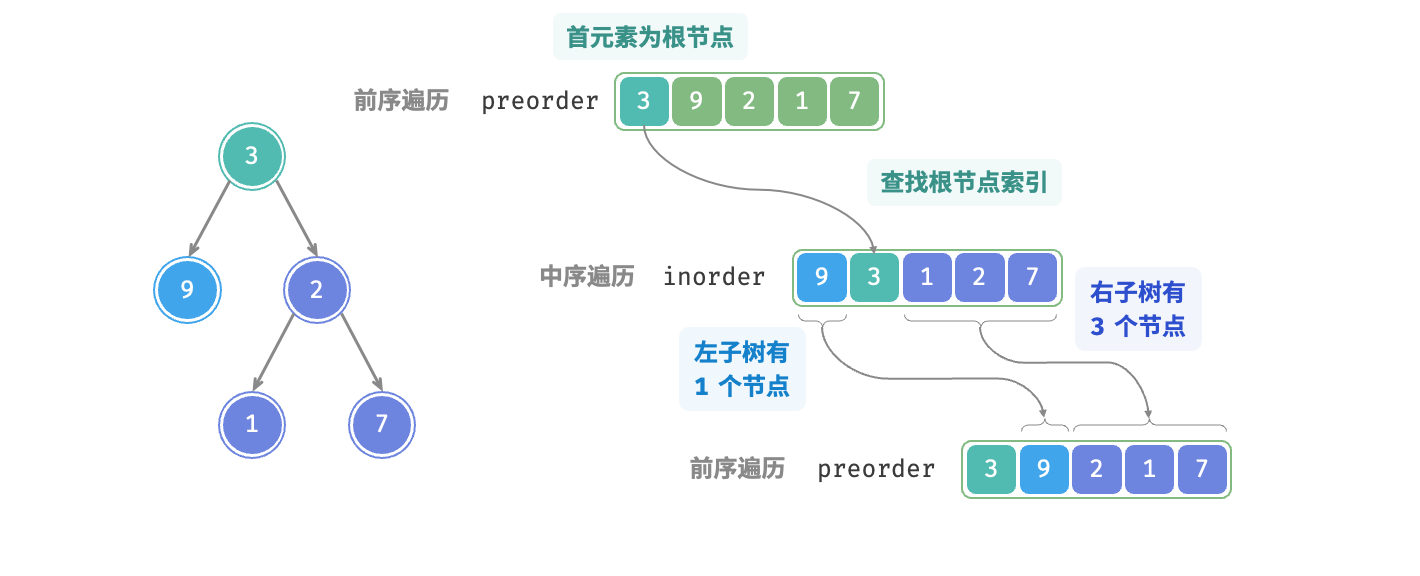
以上图数据为例,我们可以通过下图的步骤得到划分结果。
- 前序遍历的首元素3是根节点的值。
- 查找根节点3在inorder中的索引,利用该索引可将inorder划分为[ 9 | 3 | 1 2 7 ]。
- 根据inorder的划分结果,易得左子树和右子树的节点数量分别为1和3,从而可将preorder划分为[ 3 | 9 | 2 1 7 ]。
5.4 基于变量描述子树区间
根据以上划分方法,我们已经得到根节点、左子树、右子树在preorder和inorder中的索引区间。而为了描述这些索引区间,我们需要借助几个指针变量。 将当前树的根节点在preorder中的索引记为i。
将当前树的根节点在inorder中的索引记为m。
将当前树在inorder中的索引区间记为[l, r]。
如表所示,通过以上变量即可表示根节点在preorder中的索引,以及子树在inorder中的索引区间。
根节点在 preorder 中的索引 | 子树在 inorder 中的索引区间 | |
|---|---|---|
| 当前树 | i | [l,r] |
| 左子树 | i+1 | [l,m−1] |
| 右子树 | i+1+(m-l) | [m+1, r] |
请注意,右子树根节点索引中的(m-l)的含义是"左子树的节点数量"。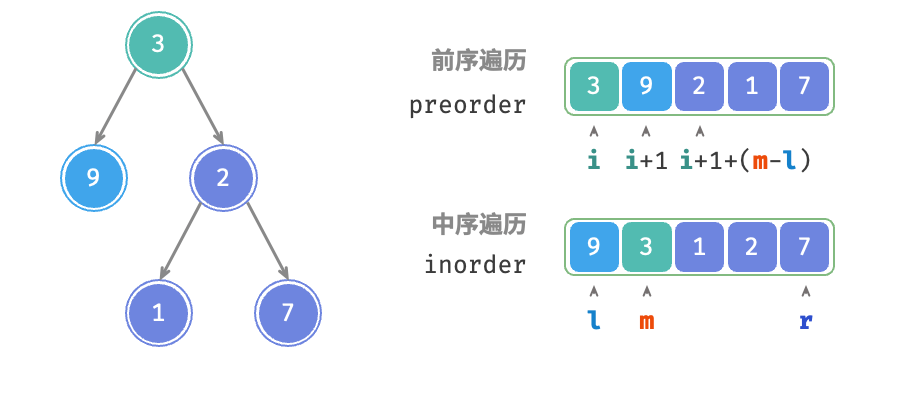
5.5 代码实现
为了提升查询m的效率,我们借助一个哈希表hmap来存储数组inorder中元素到索引的映射:
/* 构建二叉树:分治 */
TreeNode dfs(int[] preorder, Map<Integer, Integer> inorderMap, int i, int l, int r) {
// 子树区间为空时终止
if (r - l < 0)
return null;
// 初始化根节点
TreeNode root = new TreeNode(preorder[i]);
// 查询 m ,从而划分左右子树
int m = inorderMap.get(preorder[i]);
// 子问题:构建左子树
root.left = dfs(preorder, inorderMap, i + 1, l, m - 1);
// 子问题:构建右子树
root.right = dfs(preorder, inorderMap, i + 1 + m - l, m + 1, r);
// 返回根节点
return root;
}
/* 构建二叉树 */
TreeNode buildTree(int[] preorder, int[] inorder) {
// 初始化哈希表,存储 inorder 元素到索引的映射
Map<Integer, Integer> inorderMap = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
inorderMap.put(inorder[i], i);
}
TreeNode root = dfs(preorder, inorderMap, 0, 0, inorder.length - 1);
return root;
}下图展示了构建二叉树的递归过程,各个节点是在向下"递"的过程中建立的,而各条边(引用)是在向上"归"的过程中建立的。 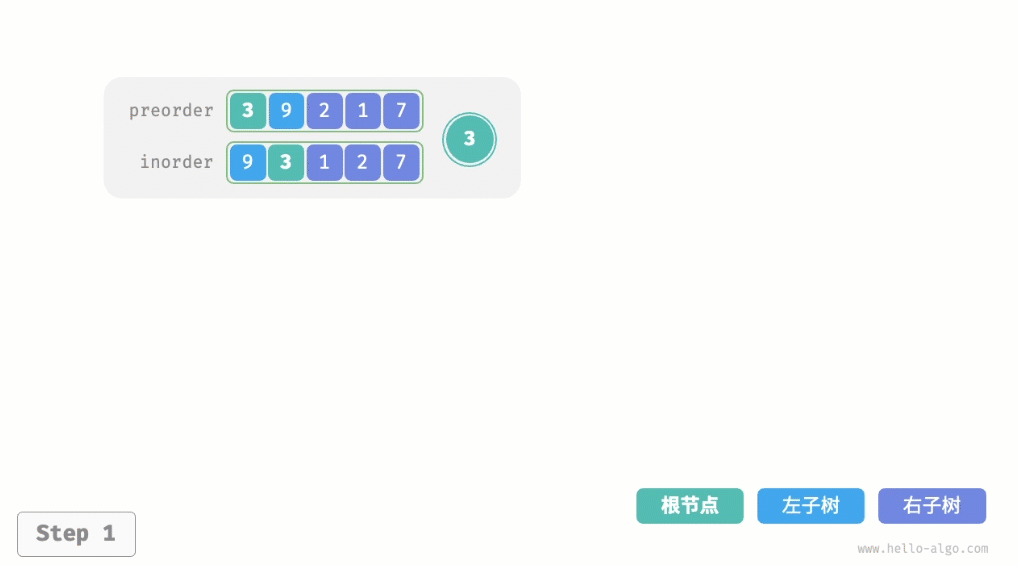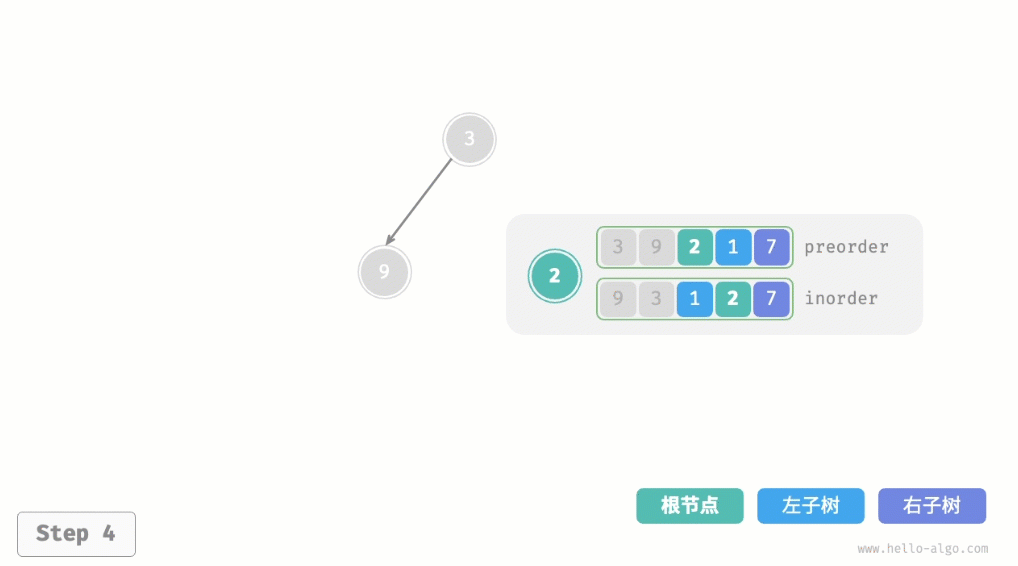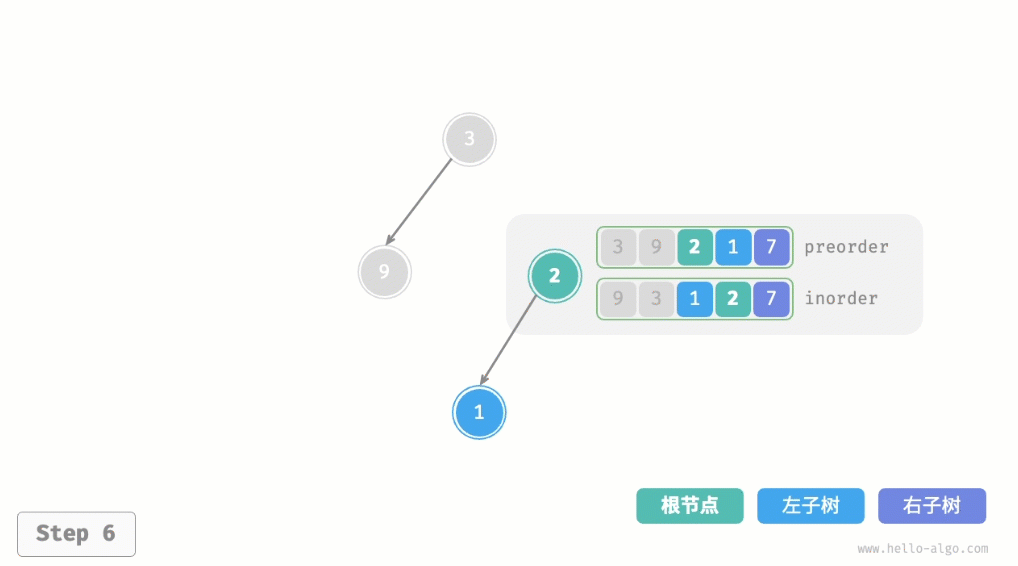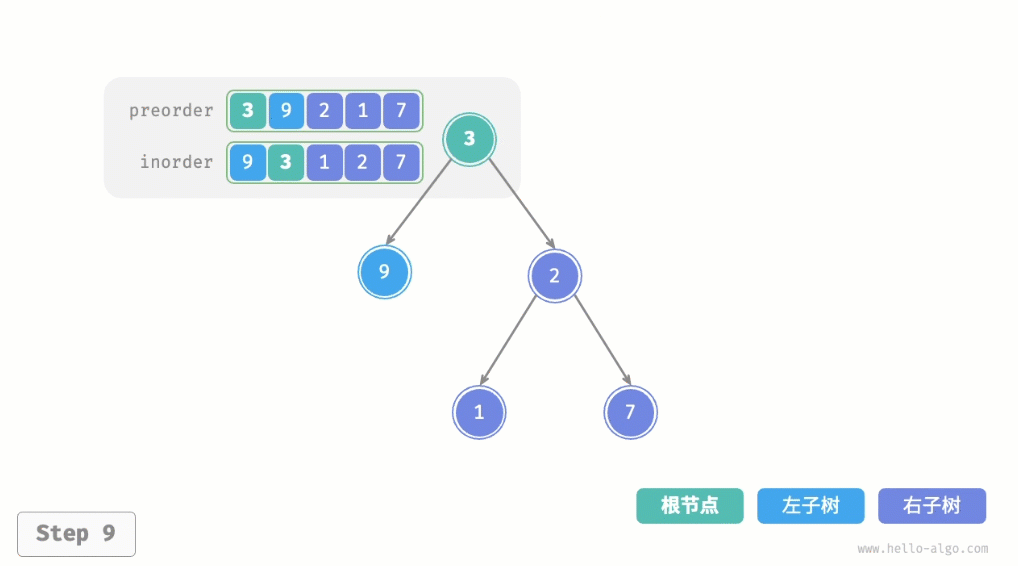 每个递归函数内的前序遍历preorder和中序遍历inorder的划分结果如图所示。
每个递归函数内的前序遍历preorder和中序遍历inorder的划分结果如图所示。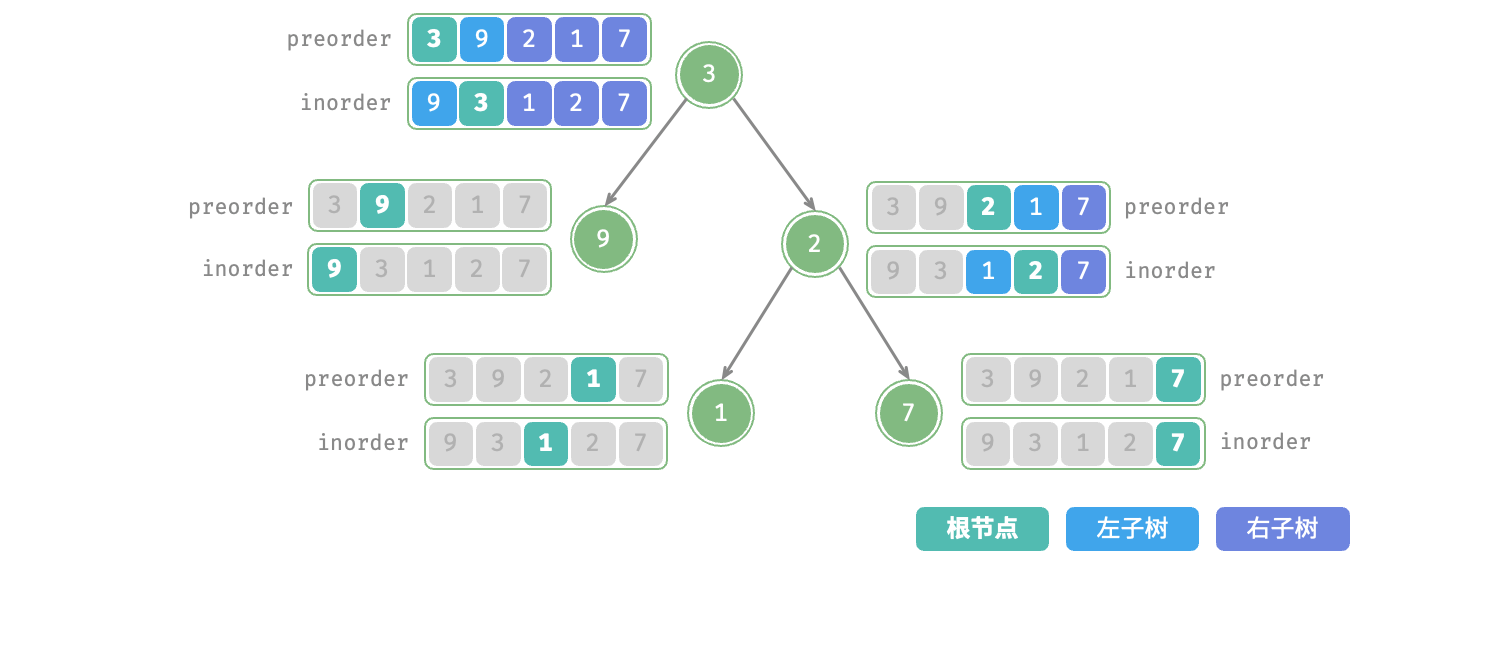 设树的节点数量为n,初始化每一个节点(执行一个递归函数dfs())使用O(1)时间。因此总体时间复杂度为O(n)。
设树的节点数量为n,初始化每一个节点(执行一个递归函数dfs())使用O(1)时间。因此总体时间复杂度为O(n)。
哈希表存储inorder元素到索引的映射,空间复杂度为O(n)。在最差情况下,即二叉树退化为链表时,递归深度达到n,使用O(n)的栈帧空间。因此总体空间复杂度为O(n)。
6. 汉诺塔问题
在归并排序和构建二叉树中,我们都是将原问题分解为两个规模为原问题一半的子问题。然而对于汉诺塔问题,我们采用不同的分解策略。
6.1 需求
给定三根柱子,记为A、B和C。起始状态下,柱子A上套着n个圆盘,它们从上到下按照从小到大的顺序排列。我们的任务是要把这n个圆盘移到柱子C上,并保持它们的原有顺序不变(如图所示)。在移动圆盘的过程中,需要遵守以下规则。
- 圆盘只能从一根柱子顶部拿出,从另一根柱子顶部放入。
- 每次只能移动一个圆盘。
- 小圆盘必须时刻位于大圆盘之上。
 我们将规模为i汉诺塔问题记作f(i)。例如f(3)代表将3个圆盘从A移动至C的汉诺塔问题。
我们将规模为i汉诺塔问题记作f(i)。例如f(3)代表将3个圆盘从A移动至C的汉诺塔问题。
6.2 考虑基本情况
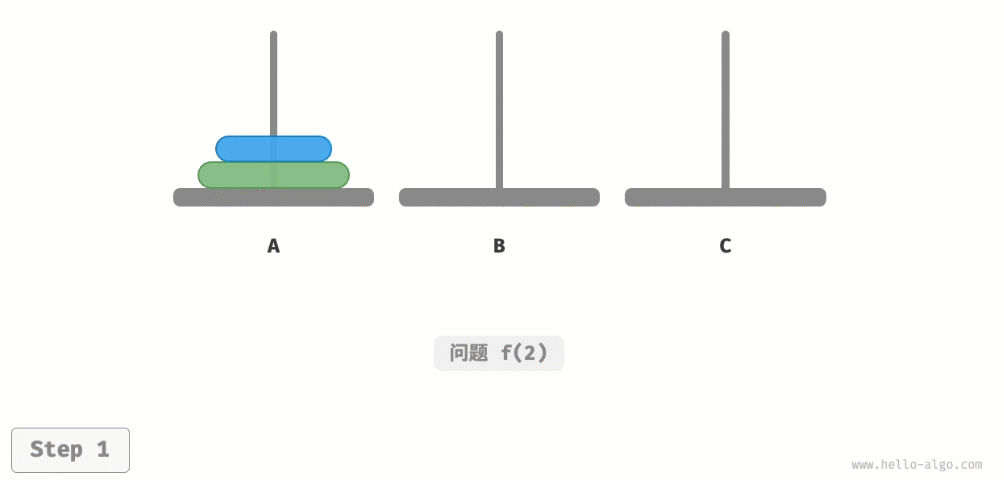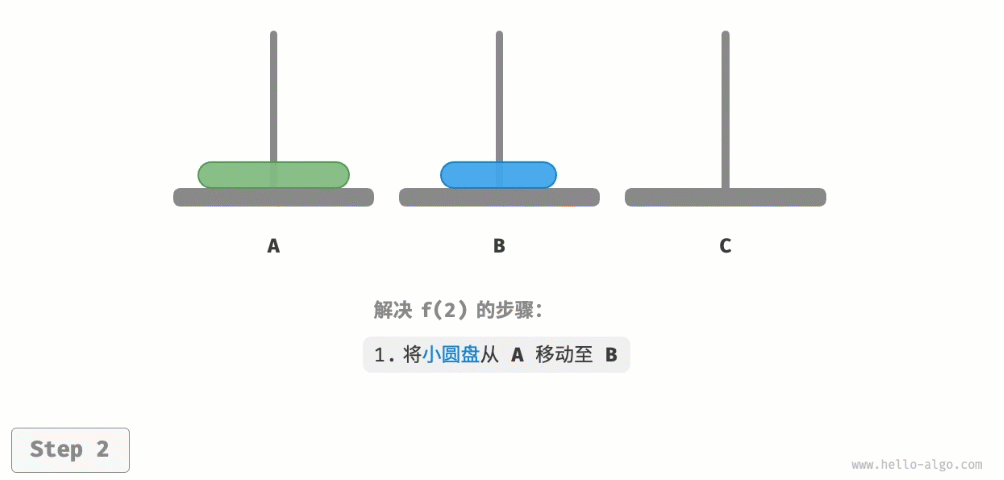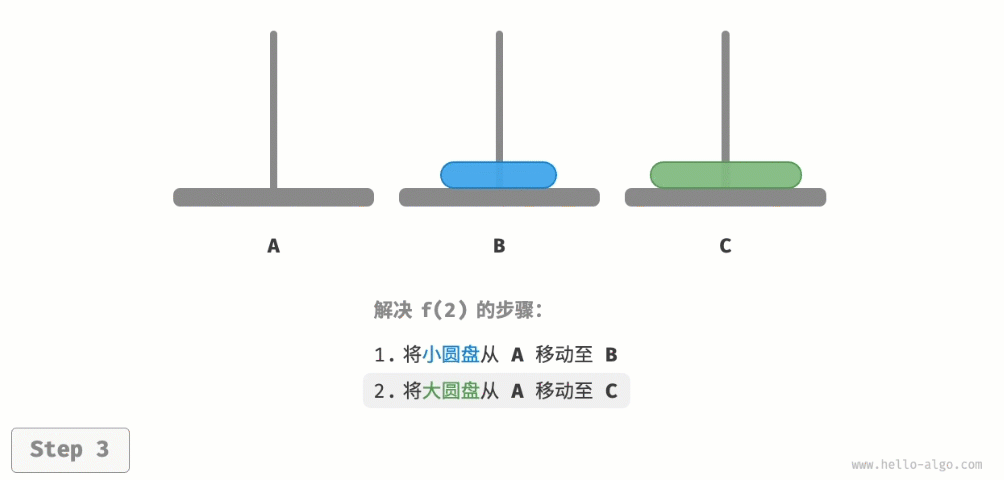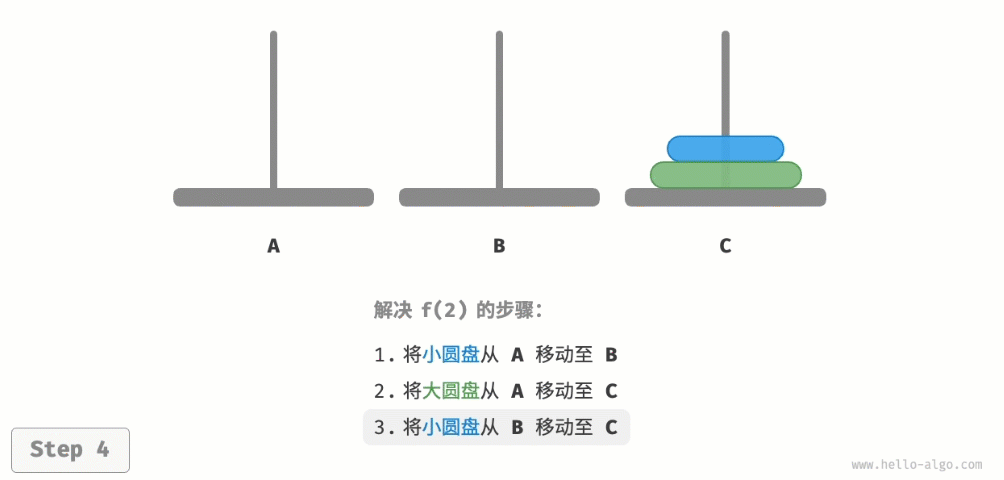
如图所示,对于问题f(1),即当只有一个圆盘时,我们将它直接从A移动至C即可。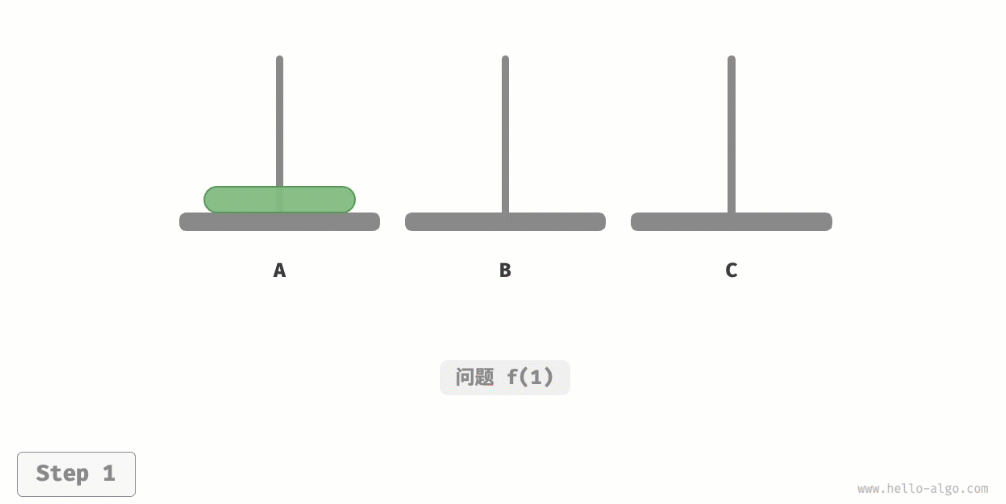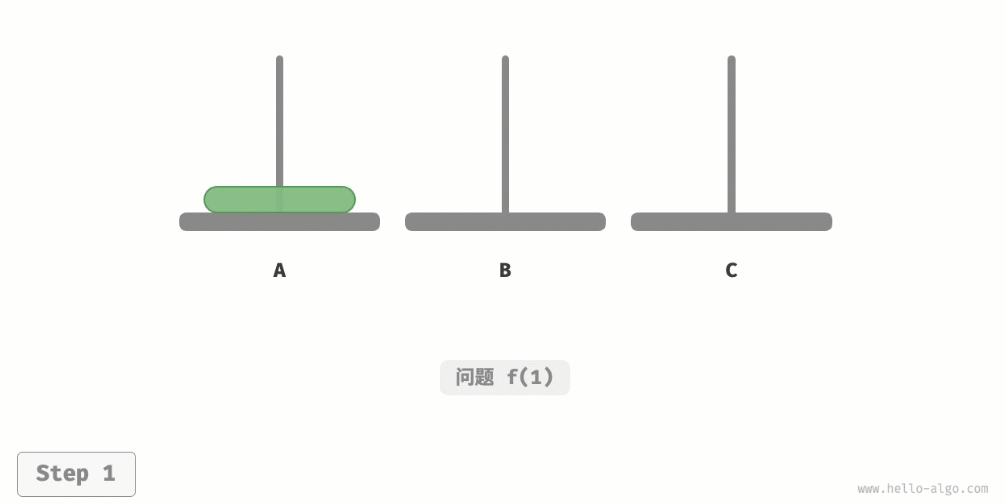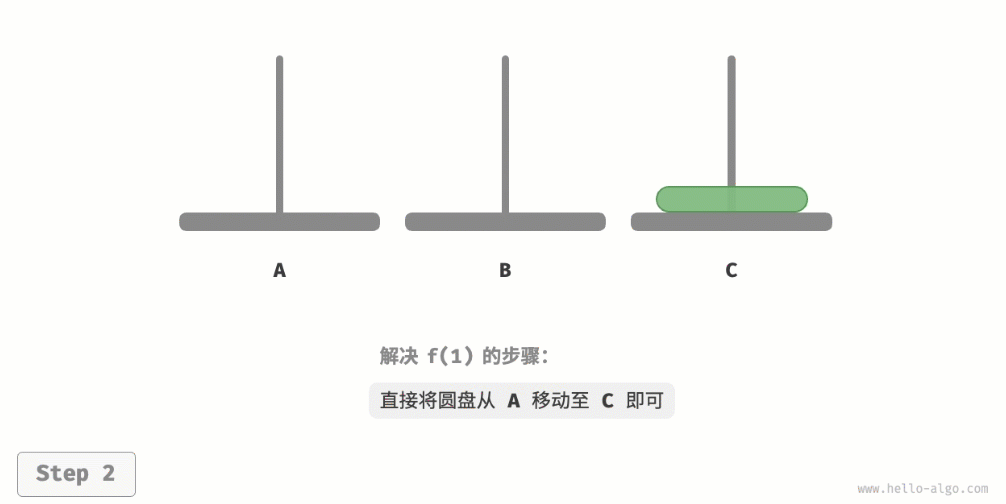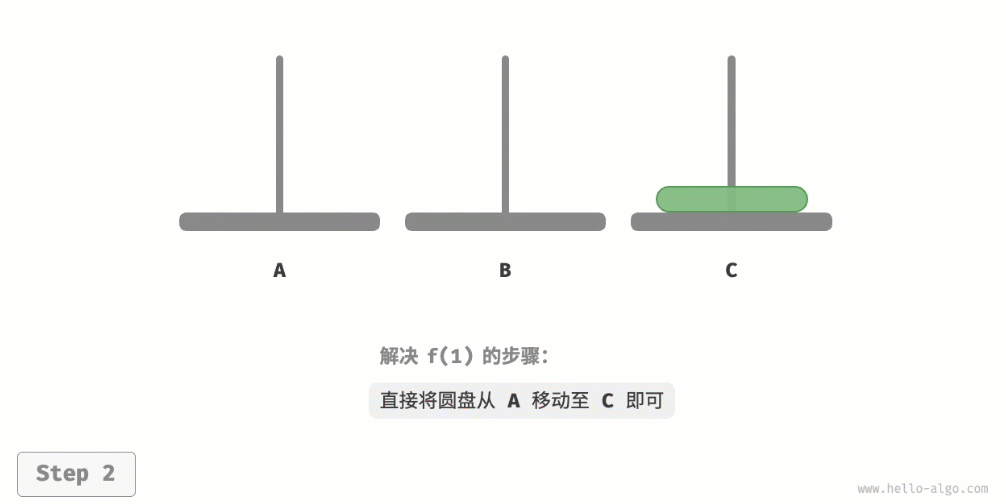 如图所示,对于问题f(2),即当有两个圆盘时,由于要时刻满足小圆盘在大圆盘之上,因此需要借助B来完成移动。
如图所示,对于问题f(2),即当有两个圆盘时,由于要时刻满足小圆盘在大圆盘之上,因此需要借助B来完成移动。
- 先将上面的小圆盘从A移至B。
- 再将大圆盘从A移至C。
- 最后将小圆盘从B移至C。
 解决问题f(2)的过程可总结为:将两个圆盘借助B从A移至C 。其中C称为目标柱、B称为缓冲柱。
解决问题f(2)的过程可总结为:将两个圆盘借助B从A移至C 。其中C称为目标柱、B称为缓冲柱。
6.3 子问题分解
对于问题f(3),即当有三个圆盘时,情况变得稍微复杂了一些。
因为已知f(1)和f(2)的解,所以我们可从分治角度思考,将A顶部的两个圆盘看作一个整体,执行图所示的步骤。这样三个圆盘就被顺利地从A移至C了。
- 令B为目标柱、C为缓冲柱,将两个圆盘从A移至B。
- 将A中剩余的一个圆盘从A直接移动至C。
- 令C为目标柱、A为缓冲柱,将两个圆盘从B移至C。
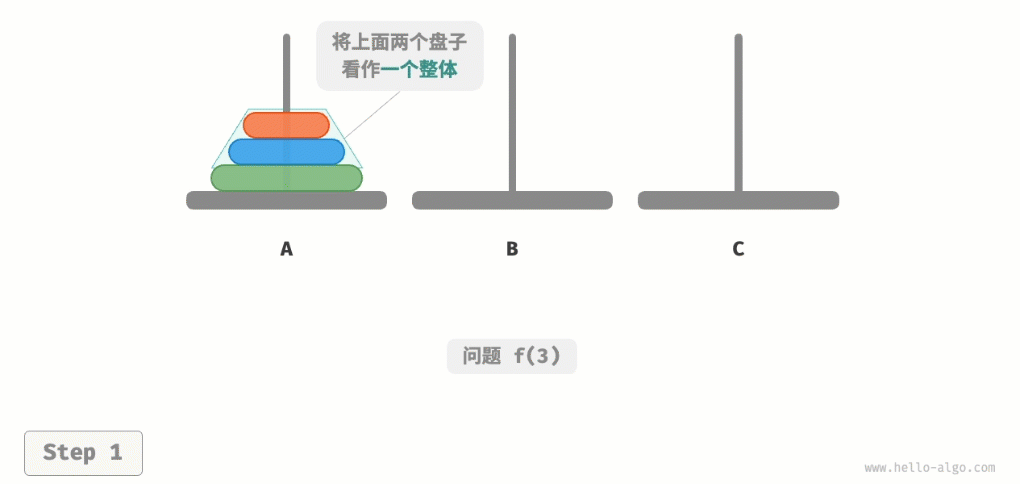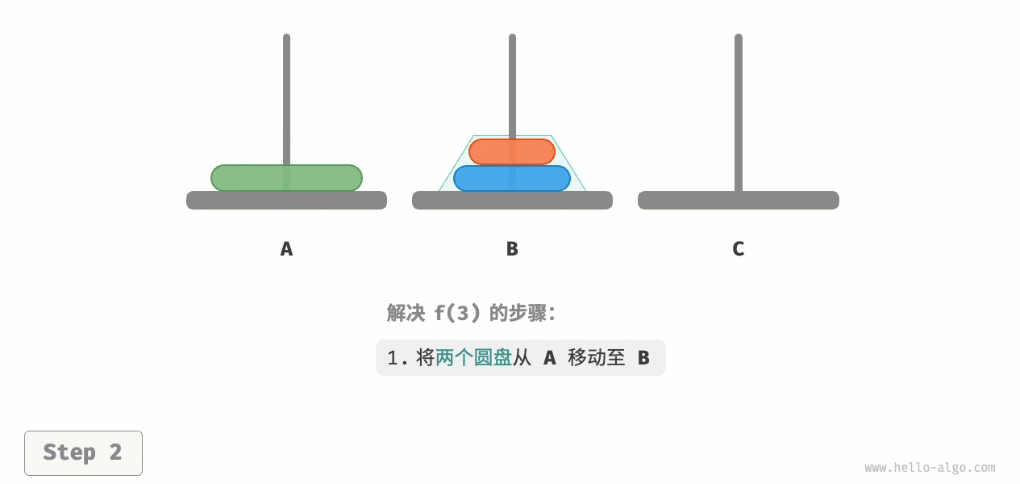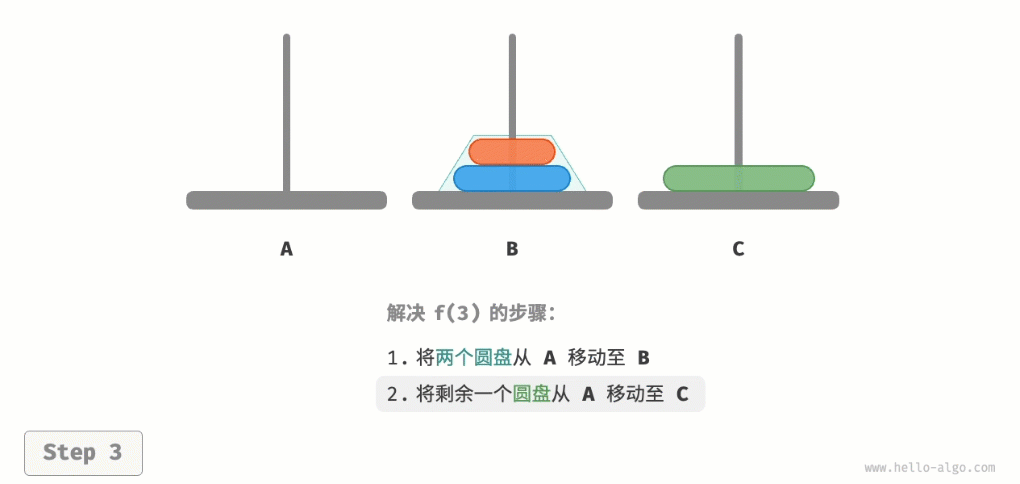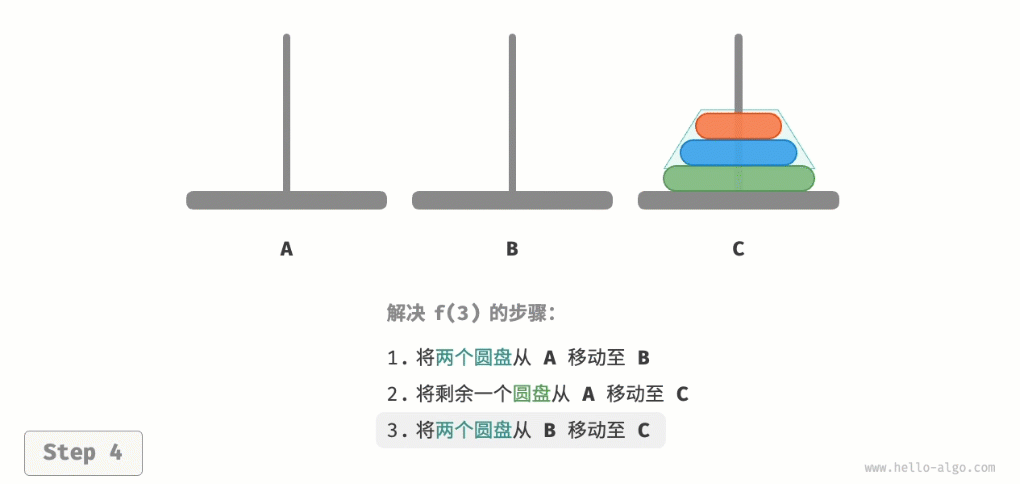 从本质上看,我们将问题f(3)划分为两个子问题f(2)和一个子问题f(1)。按顺序解决这三个子问题之后,原问题随之得到解决。这说明子问题是独立的,而且解可以合并。
从本质上看,我们将问题f(3)划分为两个子问题f(2)和一个子问题f(1)。按顺序解决这三个子问题之后,原问题随之得到解决。这说明子问题是独立的,而且解可以合并。
至此,我们可总结出下图所示的解决汉诺塔问题的分治策略:将原问题f(n)划分为两个子问题f(n-1)和一个子问题f(1),并按照以下顺序解决这三个子问题。 - 将n-1个圆盘借助C从A移至B。
- 将剩余1个圆盘从A直接移至C。
- 将n-1个圆盘借助A从B移至C。
对于这两个子问题f(n-1),可以通过相同的方式进行递归划分,直至达到最小子问题f(1)。而f(1)的解是已知的,只需一次移动操作即可。
6.4 代码实现
在代码中,我们声明一个递归函数dfs(i, src, buf, tar) ,它的作用是将柱src顶部的i个圆盘借助缓冲柱buf移动至目标柱tar:
/* 移动一个圆盘 */
void move(List<Integer> src, List<Integer> tar) {
// 从 src 顶部拿出一个圆盘
Integer pan = src.remove(src.size() - 1);
// 将圆盘放入 tar 顶部
tar.add(pan);
}
/* 求解汉诺塔问题 f(i) */
void dfs(int i, List<Integer> src, List<Integer> buf, List<Integer> tar) {
// 若 src 只剩下一个圆盘,则直接将其移到 tar
if (i == 1) {
move(src, tar);
return;
}
// 子问题 f(i-1) :将 src 顶部 i-1 个圆盘借助 tar 移到 buf
dfs(i - 1, src, tar, buf);
// 子问题 f(1) :将 src 剩余一个圆盘移到 tar
move(src, tar);
// 子问题 f(i-1) :将 buf 顶部 i-1 个圆盘借助 src 移到 tar
dfs(i - 1, buf, src, tar);
}
/* 求解汉诺塔问题 */
void solveHanota(List<Integer> A, List<Integer> B, List<Integer> C) {
int n = A.size();
// 将 A 顶部 n 个圆盘借助 B 移到 C
dfs(n, A, B, C);
}如图所示,汉诺塔问题形成一棵高度为n的递归树,每个节点代表一个子问题,对应一个开启的dfs()函数,因此时间复杂度为O(n²),空间复杂度为O(n)。 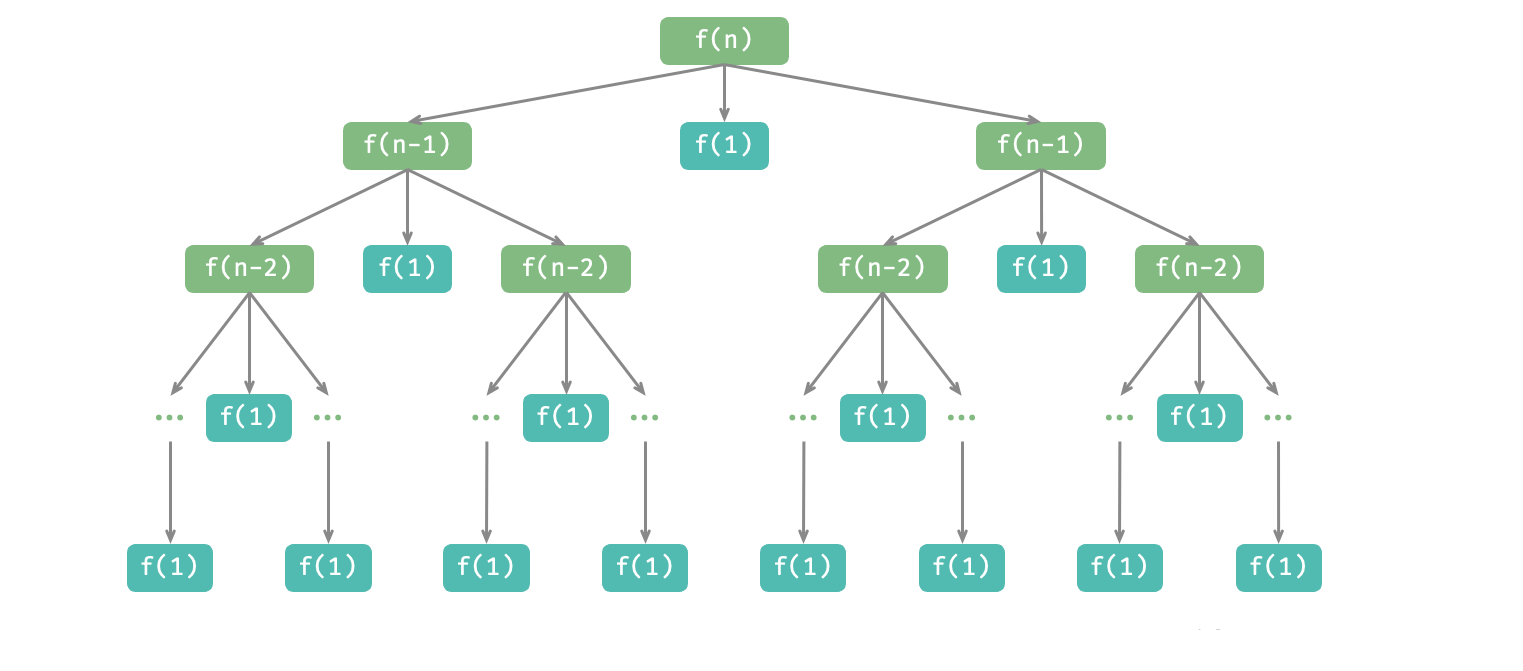
提示
汉诺塔问题源自一个古老的传说。在古印度的一个寺庙里,僧侣们有三根高大的钻石柱子,以及64个大小不一的金圆盘。僧侣们不断地移动圆盘,他们相信在最后一个圆盘被正确放置的那一刻,这个世界就会结束。
然而,即使僧侣们每秒钟移动一次,总共需要大约2⁶⁴≈1.84x10¹⁹秒,合约5850亿年,远远超过了现在对宇宙年龄的估计。所以,倘若这个传说是真的,我们应该不需要担心世界末日的到来。
