数据结构总览

1. 数据结构分类

常见的数据结构包括数组、链表、栈、队列、哈希表、树、堆、图，它们可以从"逻辑结构"和"物理结构"两个维度进行分类。

1.1 逻辑结构：线性与非线性

逻辑结构揭示了数据元素之间的逻辑关系。逻辑结构可分为"线性"和"非线性"两大类。线性结构比较直观，指数据在逻辑关系上呈线性排列；非线性结构则相反，呈非线性排列。
线性数据结构：数组、链表、栈、队列、哈希表，元素之间是一对一的顺序关系。
非线性数据结构：树、堆、图、哈希表。

非线性数据结构可以进一步划分为树形结构和网状结构：
树形结构：树、堆、哈希表，元素之间是一对多的关系。
网状结构：图，元素之间是多对多的关系。

1.2 物理结构：连续与分散

当算法程序运行时，正在处理的数据主要存储在内存中，系统通过内存地址来访问目标位置的数据。内存是所有程序的共享资源，当某块内存被某个程序占用时，则通常无法被其他程序同时使用了。因此在数据结构与算法的设计中，内存资源是一个重要的考虑因素。
如图所示，物理结构反映了数据在计算机内存中的存储方式，可分为连续空间存储(数组)和分散空间存储(链表)。物理结构从底层决定了数据的访问、更新、增删等操作方法，两种物理结构在时间效率和空间效率方面呈现出互补的特点。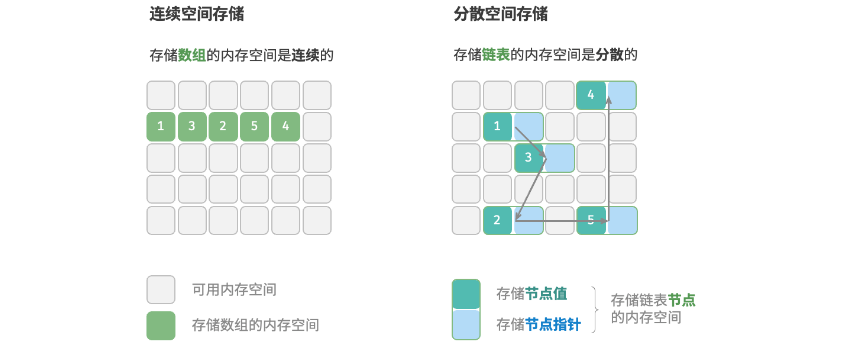
值得说明的是，所有数据结构都是基于数组、链表或二者的组合实现的, 具体如下：

• 基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量(维度>2的数组)等。
• 基于链表可实现：栈、队列、哈希表、树、堆、图等。
  链表在初始化后，仍可以在程序运行过程中对其长度进行调整，因此也称"动态数据结构"。数组在初始化后长度不可变，因此也称"静态数据结构"。值得注意的是，数组可通过重新分配内存实现长度变化，从而具备一定的"动态性"。

2. 基本数据类型

基本数据类型是 CPU 可以直接进行运算的类型，在算法中直接被使用，主要包括以下几种:

• 整数类型: byte、short、int、long。
• 浮点数类型: float、double ，用于表示小数。
• 字符类型: char ，用于表示各种语言的字母、标点符号甚至表情符号等。
• 布尔类型: bool ，用于表示"是"与"否"判断。
  基本数据类型的取值范围取决于其占用的空间大小。下面以 Java 为例:
  整数类型byte占用1字节=8比特 ，可以表示2^8个数字。整数类型int占用4字节=32比特 ，可以表示2^32个数字。
  基本数据类型与数据结构之间有什么联系呢？
  基本数据类型提供了数据的"内容类型"，而数据结构提供了数据的"组织方式"。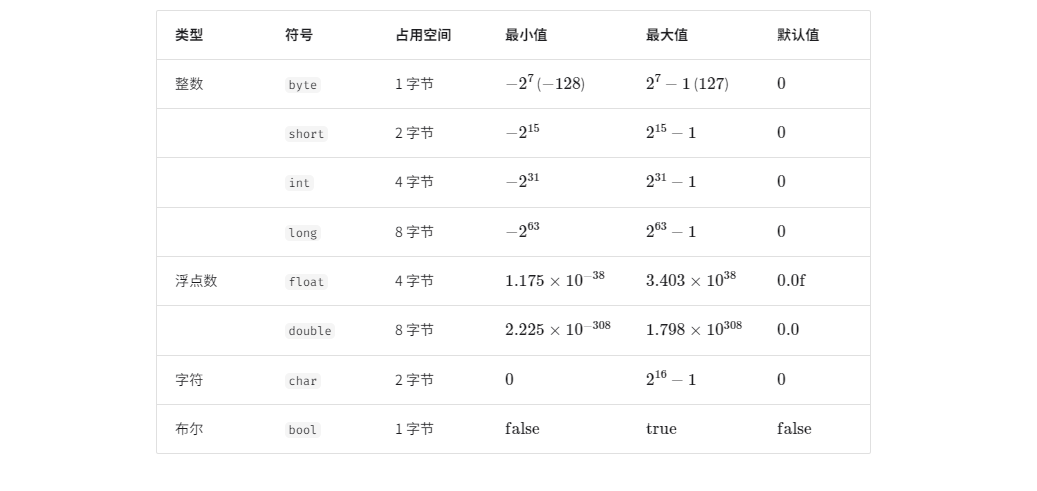

3. 数据编码

3.1 原码、反码和补码

所有整数类型能够表示的负数都比正数多一个，例如byte的取值范围是[-127,128]。这个现象比较反直觉，它的内在原因涉及原码、反码、补码的相关知识。首先需要指出，数字是以"补码"的形式存储在计算机中的。

• 原码：我们将数字的二进制表示的最高位视为符号位，其中0表示正数，1表示负数，其余位表示数字的值。
• 反码：正数的反码与其原码相同，负数的反码是对其原码除符号位外的所有位取反。
• 补码：正数的补码与其原码相同，负数的补码是在其反码的基础上加1。
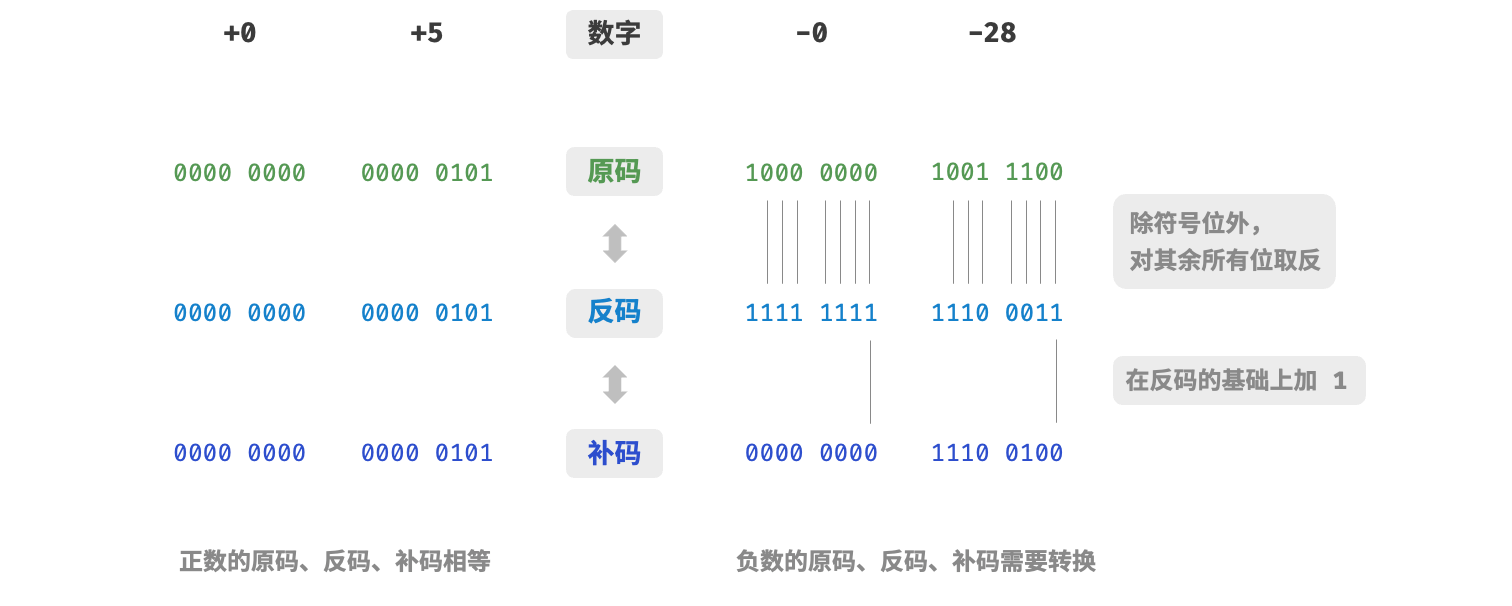  原码(sign-magnitude)虽然最直观，但存在一些局限性。一方面负数的原码不能直接用于运算。例如在原码下计算1+(-2), 得到的结果是-3,这显然是不对的。 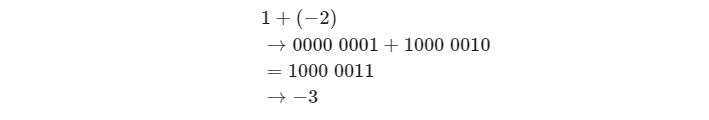为了解决此问题，计算机引入了反码,如果我们先将原码转换为反码，并在反码下计算1+(-2), 最后将结果从反码转换回原码，则可得到正确结果-1。
  另一方面，数字零的原码有+0和-0两种表示方式。这意味着数字零对应两个不同的二进制编码，这可能会带来歧义。比如在条件判断中，如果没有区分正零和负零，则可能会导致判断结果出错。而如果我们想处理正零和负零歧义，则需要引入额外的判断操作，这可能会降低计算机的运算效率。
  与原码一样，反码也存在正负零歧义问题，因此计算机进一步引入了补码。我们先来观察一下负零的原码、反码、补码的转换过程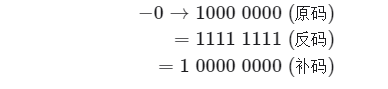： 在负零的反码基础上加1会产生进位，但byte类型的长度只有8位，因此溢出到第9位的1会被舍弃。也就是说，负零的补码为00000000，与正零的补码相同。这意味着在补码表示中只存在一个零，正负零歧义从而得到解决。
  还剩最后一个疑惑：byte类型的取值范围是[-128, 127]，多出来的一个负数-128是如何得到的呢？我们注意到，区间[-127,+127]内的所有整数都有对应的原码、反码和补码，并且原码和补码之间可以互相转换。然而，补码10000000是一个例外，它并没有对应的原码。根据转换方法，我们得到该补码的原码为00000000。这显然是矛盾的，因为该原码表示数字0，它的补码应该是自身。计算机规定这个特殊的补码10000000代表-128。

3.2 浮点数编码

细心的你可能会发现：int和float长度相同，都是4字节 ，但为什么float的取值范围远大于int？这非常反直觉，因为按理说float需要表示小数，取值范围应该变小才对。
实际上，这是因为浮点数float采用了不同的表示方式。记一个 32 比特长度的二进制数为： 根据IEEE 754标准，32-bit长度的float由以下三个部分构成:

• 符号位S: 占1位, 对应b₃₁
• 指数位E: 占8位, 对应b₃₀b₂₉...b₂₃
• 分数位N: 占23位, 对应b₂₂b₂₁...b₀
  二进制数float对应值的计算方法为：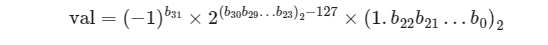
  转化到十进制下的计算公式为： 双精度double也采用类似于float的表示方法。

4. 字符编码

在计算机中，所有数据都是以二进制数的形式存储的，字符char也不例外。为了表示字符，我们需要建立一套"字符集"，规定每个字符和二进制数之间的一一对应关系。有了字符集之后，计算机就可以通过查表完成二进制数到字符的转换。

4.1 ASCII字符集

ASCII 码是最早出现的字符集，其全称为 American Standard Code for Information Interchange(美国标准信息交换代码)。它使用7位二进制数(一个字节的低7位)表示一个字符，最多能够表示128个不同的字符。ASCII码包括英文字母的大小写、数字0~9、一些标点符号，以及一些控制字符(如换行符和制表符)。

4.2 GBK字符集

然而，ASCII 码仅能够表示英文。比如汉字有近十万个，光日常使用的就有几千个。中国国家标准总局于1980年发布了GB2312字符集，其收录了6763个汉字，基本满足了汉字的计算机处理需要。然而，GB2312无法处理部分罕见字和繁体字。GBK字符集是在GB2312的基础上扩展得到的，它共收录了21886个汉字。在GBK的编码方案中，ASCII字符使用一个字节表示，汉字使用两个字节表示。

4.3 Unicode字符集

Unicode 的中文名称为"统一码"，理论上能容纳100多万个字符。它致力于将全球范围内的字符纳入统一的字符集之中，提供一种通用的字符集来处理和显示各种语言文字，减少因为编码标准不同而产生的乱码问题。Unicode是一种通用字符集，本质上是给每个字符分配一个编号(称为"码点")，但它并没有规定在计算机中如何存储这些字符码点。一种直接的解决方案是将所有字符存储为等长的编码。但是英文和数字不需要大于1个字节进行保存，因此，我们需要一种更加高效的Unicode编码方法。

4.4 UTF-8编码

目前，UTF-8已成为国际上使用最广泛的 Unicode 编码方法。它是一种可变长度的编码，使用1到4字节来表示一个字符，根据字符的复杂性而变。ASCII字符只需1字节，拉丁字母和希腊字母需要2字节，常用的中文字符需要3字节，其他的一些生僻字符需要4字节。